<<
Back to Kanarev's Physchemistry Book Index
10.6. Structure of the Beryllium Atom
When we define the
structure of the atoms, we are guided by the results of the analysis of experimental
optical spectroscopy, from which it appears that the electron in the atom has
no orbital movement and interacts with the nucleus with the axis of its
rotation. Please, pay attention to the structure of the symmetrical nucleus of
the beryllium atom (Fig. 26). It consists of four protons and five neutrons.
The atom of the
chemical element beryllium is also symmetrical as its nucleus (Fig. 57). As all
four protons of the nucleus are situated on its surface and each of them has
one free magnetic pole, the electrons are connected to these poles.
Let us make a table
of binding energies of all electrons of the beryllium atom (Table 33). Let us
remind that binding energy of the first electron of this atom with the nucleus,
which corresponds to the first energy
level, is equal to 
=64.67 eV, of the second one - 
=56.26 eV, of the third one - 
=120.89 eV, of the fourth one - 
=217.71 eV.
Table 33. Binding
energy 
of the electron of
the hydrogen atom 
and of the first, the
second, the third and the fourth electrons of the beryllium atom Be with the
nucleus
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
13.6 |
3.40 |
1.51 |
0.85 |
0.54 |
0.38 |
0.28 |
0.21 |
0.17 |
|
1 |
16.17 |
4.04 |
1.80 |
1.01 |
0.65 |
0.45 |
0.33 |
0.25 |
0.20 |
|
2 |
56.26 |
14.06 |
6.25 |
3.52 |
2.25 |
1.56 |
1.15 |
0.88 |
0.69 |
|
3 |
120.89 |
30.22 |
13.43 |
7.56 |
4.83 |
3.36 |
2.47 |
1.89 |
1.49 |
|
4 |
217.71 |
54.43 |
24.19 |
13.6 |
8.71 |
6.05 |
4.44 |
3.40 |
2.69 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
0.14 |
0.11 |
0.09 |
0.08 |
0.07 |
0.06 |
0.05 |
0.05 |
0.04 |
|
1 |
0.16 |
0.12 |
0.10 |
0.08 |
0.07 |
0.06 |
0.05 |
0.05 |
0.04 |
|
2 |
0.56 |
0.46 |
0.39 |
0.33 |
0.29 |
0.25 |
0.22 |
0.19 |
0.17 |
|
3 |
1.21 |
1.00 |
0.84 |
0.72 |
0.62 |
0.54 |
0.47 |
0.42 |
0.37 |
|
4 |
2.18 |
1.80 |
1.51 |
1.29 |
1.11 |
0.97 |
0.85 |
0.75 |
0.67 |
As
example we calculate the binding energy for the forth electron and its
14-th energy level. 
(see Table 33).
For the third electron and its 17-th energy level we have 
(see Table 33).
We’ll not give
similar calculations according to the formulas (247) and (248) for all electrons,
but we’ll note that the determined regularities remain in this case as well. It
is natural that the calculation error is increased when the atom and its
nucleus become more complicated. It is explained by the fact that when the atom
and its nucleus become more complicated. It is explained by the fact that when
one or two electrons interact with the nucleus of the atom with many protons
the screening effect of the neutrons is increased. The analysis of regularity
of this increase waits for its investigator.
The analysis of
Table 33 shows that when the number of energy level is increased in the spectra
of the second, the third and the fourth electrons, the energy values appear,
which are close to the energy values of the hydrogen atom at its high energy
levels. Indirectly, it proves the fact that if all electrons are in the atom,
their binding energies with the nuclei are approximately equal and close to
binding energies of the electron of the hydrogen atom with its nucleus. It is a
very important consequence. It points out to the fact that each electron of one
atom can be connected with the electrons of another atom generating almost
similar binding energies on the like energy levels.
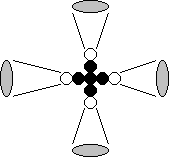
2
1 3
4
Fig. 57. Diagram of
the structure of the beryllium nucleus and atom: 1, 2, 3 and 4 are the numbers
of the electrons
In connection with
the above-mentioned facts, a question arises: is it reasonable to calculate
binding energies of all electrons of the atom taking into account ionization
energy of each of them? It is unlikely.
Binding energies calculated in such a way belong to such state of the atom when
one, two and more electrons are absent in it. In such a state, the atom can be
at the temperature, which brings it into a plasma state. As this state
corresponds to a very high temperature, at which usually no chemical reactions
take place, the necessity in such calculation is reduced.
It is much more
important to know binding energies of any electron of any atom for the sate
when the majority of chemical reactions take place. In such state the atom has
all electrons, and their binding energies with the nuclei are close to binding
energies of the electron of the hydrogen atom. That’s why during further
analysis of the structures of the atoms we’ll calculate the spectra and
determine binding energies with the atomic nuclei only for the first electrons,
which have the least ionization potential. They are the main valency electrons
of the atoms.
10.7. Structure of
the Boron Atom
The boron atom is
the fifth element in the periodic law. The majority of the nuclei of this atom
have five protons and six neutrons (Fig. 25, b). The nucleus of the boron atom
has one axis of symmetry. The atom of this chemical element has similar
structure (Fig. 58). Five protons have free magnetic poles, to which the
electrons are attached.
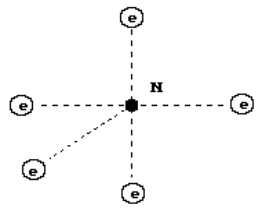
Fig. 58. Structure
of the Boron atom
The axis of the
first electron, which passes through the atomic nucleus, is the only axis of
its symmetry. Later on, we’ll see that more complicated atoms have several axes
of symmetry.
10.8. Structure of
the Carbon Atom
Carbon is
considered to the basis of life, because it forms the largest number of bonds
with the atoms of other chemical elements. Let us define the cause of its
activity. The nucleus of the carbon atom has two forms. The first form of the
nucleus, which includes six neutrons, forms the atoms of graphite (Fig. 26, a).
The second, spatial form of the nucleus has seven neutrons. It forms the nuclei
of diamond (Fig. 26, b). Each proton has a free magnetic pole to be connected
with the electron.
All six protons of
the nucleus of the carbon atom and its all six electrons of the atom have equal
possibilities to be connected with the electrons of other atoms and to form
complex combinations. The carbon atoms with a flat nucleus (Fig. 59, a) form
organic combinations, in which all six electrons of this atom take part in the
formation of bonds between the atoms of various molecules.
The structure of
the atom of diamond, which is formed from the spatial nucleus of this atom, has
free axes of symmetry (Fig. 59, b). They are the axes of the Cartesian coordinate
system. The structure of spatial nucleus and atom of carbon and the atom itself
demonstrate the main property of diamond: its strength.
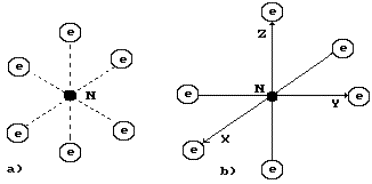
Fig. 59. Flat a)
and spatial b) structure of the carbon atom: N is nucleus; e are electrons; XYZ
are the axes of the Cartesian coordinate system
10.9. Structure of
Nitrogen Atom
Nitrogen is the
seventh element in the periodic law of elements arranged in its fifth period.
Structure of its nucleus is shown in Fig. 27. In its form, it is similar to the
structure of the carbon atom. As the majority of the nuclei of the nitrogen
atoms have seven protons and seven neutrons, this majority has flat nucleus
shown in Fig. 27, a. The diagram of the nitrogen atom, which has such nucleus,
is shown in Fig. 60.
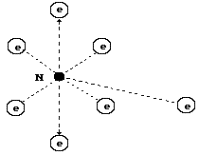
Fig. 60. Diagram of
the nitrogen atom: N is the atomic nucleus;
e are the atomic electrons
10.10. Structure of
the Oxygen Atom and Molecule
The oxygen atom is
the eighth element of the periodic law of chemical elements arranged in its
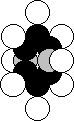
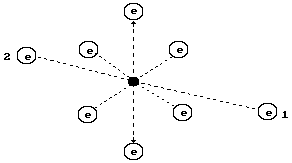
sixth group (Fig. 61). The structure of its nucleus is shown in Fig. 28.
Symmetry of the nucleus should be transferred to the atom. The most probable
diagram of the oxygen atom is given in Fig. 61. It has eight electrons; the
ones, which are situated on the axis of symmetry, are the most active ones (1
and 2). Six other electrons arranged in the plane, which is perpendicular to
the axis line (the line of symmetry) remove the electrons 1 and 2 from the
nucleus by its total electrical field at a long distance forming the conditions
for their large activity during the interaction with the electrons of the
neighboring atoms.
The structure of
the oxygen molecule is shown in Fig. 62. It is formed by means of connection of
the unlike magnetic poles of the axis electrons of two oxygen atoms.
As it is clear, the
oxygen molecule has fourteen free electrons, which are ready to be connected.
It is likely that the axis electrons 1’ and 2 are the ones, which are the most
remote from the structure of the whole molecule, they are the most active ones,
i.e. they are capable to be connected with the electrons of other atoms.
a)
b)
Fig. 61. Diagram of
the nucleus (a) and oxygen atom (b)
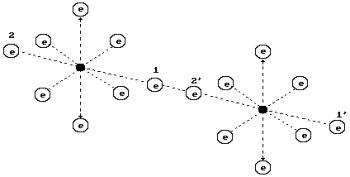
Fig. 62. Diagram of
the oxygen molecule model 
The electrons of
the flat carbon atoms have large binding energies with the nuclei, and they are
less active. When they become excited, their activity is considerably increased,
and they start being connected with the electrons of the atoms of other
chemical elements.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index