<<
Back to Kanarev's Physchemistry Book Index
10.3.
Models of the Hydrogen Molecule
As the temperature
is reduced, the electrons of the hydrogen atoms move to lower energy levels
(come close to the protons). Their bond with the protons becomes stronger, and
the conditions appear for the connection into a unified structure of two
protons and two electrons. But prior to it the formation of an intermediate
structure ![]() is possible , which
is called a molecular ion of hydrogen. The structure of such ion is given in
Fig. 52 [2], [52]. Let us pay attention to the formation of its spin.
is possible , which
is called a molecular ion of hydrogen. The structure of such ion is given in
Fig. 52 [2], [52]. Let us pay attention to the formation of its spin.
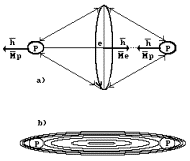
Fig. 52. Diagram of molecular
ion ![]() : a) originates from our theory; b) originates from Schroedinger’s
equation
: a) originates from our theory; b) originates from Schroedinger’s
equation
As in general
vectors of angular momentum ![]() and magnetic moment
and magnetic moment ![]() coincide in their
direction and as the like magnetic poles of the electron and the first proton
are directed to meet each other, vectors of their angular momentum
coincide in their
direction and as the like magnetic poles of the electron and the first proton
are directed to meet each other, vectors of their angular momentum ![]() are directed to meet
each other, that’s why their sum is equal to zero. Vector of angular momentum
of the second proton remains uncompensated, that’s why spin of molecular ion of
hydrogen
are directed to meet
each other, that’s why their sum is equal to zero. Vector of angular momentum
of the second proton remains uncompensated, that’s why spin of molecular ion of
hydrogen ![]() is equal to Planck’s
constant. The directions of vectors of magnet moments of both protons coincide,
that’s why magnet moment of ion
is equal to Planck’s
constant. The directions of vectors of magnet moments of both protons coincide,
that’s why magnet moment of ion ![]() is reduced as
compared with magnet moment of the hydrogen atom by a value of magnet movement
of the second proton and becomes equal
to
is reduced as
compared with magnet moment of the hydrogen atom by a value of magnet movement
of the second proton and becomes equal
to ![]()
Molecular ion of
hydrogen is unstable formation as well, because its second proton has weaker
connection with the electron and, therefore, it has a stock of free
electromagnetic lines in order to be connected with free electron, and this
phenomenon does not take place. Hydrogen molecule ![]() is formed
(Fig. 53). Magnetic and electrical lines of force interact with each other,
that’s why such structure is chemically inactive at usual temperature.
is formed
(Fig. 53). Magnetic and electrical lines of force interact with each other,
that’s why such structure is chemically inactive at usual temperature.
Two protons and two
electrons, as it is accepted in modern chemistry, form the structure with
rather strong bond equal to 436 kJ/mol. In calculation for one molecule it will
be
![]() , (246)
, (246)
and for one atom –
2.26 eV.
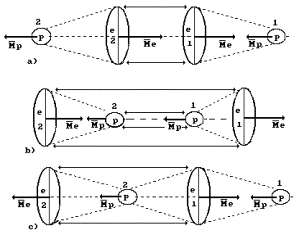
Fig. 53. Diagram of the hydrogen molecule ![]() : a), b) – orthohydrogen, c) – parahydrogen
: a), b) – orthohydrogen, c) – parahydrogen
Let us pay
attention to an important thing. According to the existing notions, the
hydrogen molecule can have two structures. In the structure of orthohydrogen,
the directions of vectors of magnetic moments of the protons are turned to one
direction, and in the structure of parahydrogen to opposite directions [2]. But
we have already shown that the value of magnetic moment of the proton is by a
factor of ![]() less than the value
of magnetic moment of the electron, that’s why the hydrogen molecule
classification adopted in modern chemistry should be determined not by magnetic
moment of the proton, but by magnetic moment of the electron. If this
peculiarity is taken into consideration, the hydrogen molecule will have the
following difference in its structure.
less than the value
of magnetic moment of the electron, that’s why the hydrogen molecule
classification adopted in modern chemistry should be determined not by magnetic
moment of the proton, but by magnetic moment of the electron. If this
peculiarity is taken into consideration, the hydrogen molecule will have the
following difference in its structure.
In Fig. 53, a, b, the directions of vectors of
magnetic moments ![]() of both electrons coincide;
it means that the directions of vectors of their angular momentum
of both electrons coincide;
it means that the directions of vectors of their angular momentum ![]() coincide. Let us call
the structure orthohydrogen. In Fig. 53, c the above-mentioned vectors are opposite,
that’s why let us call this structure parahydrogen [2].
coincide. Let us call
the structure orthohydrogen. In Fig. 53, c the above-mentioned vectors are opposite,
that’s why let us call this structure parahydrogen [2].
Let us pay attention
to the logical actions of the Nature connected with orthohydrogen structure
formation (Fig. 53, a). Electro static forces of mutual attraction of the first
electron and the first proton are balanced by magnetic forces of these
particles turned to opposite directions. That’s why vectors `![]() and
and ![]() of their magnetic moments
are turned to opposite directions. Electrostatic forces of repulsion existing between
the first electron and the second one are balanced by magnetic forces
converging them, that’s why the direction of vectors `
of their magnetic moments
are turned to opposite directions. Electrostatic forces of repulsion existing between
the first electron and the second one are balanced by magnetic forces
converging them, that’s why the direction of vectors `![]() of their magnetic moments coincide. In order to compensate
for electrostatic forces of mutual attraction of the second electron and the
second proton, it is necessary to make magnetic forces of these particles
opposite directed ones. This action is reflected in opposite directed
vectors
of their magnetic moments coincide. In order to compensate
for electrostatic forces of mutual attraction of the second electron and the
second proton, it is necessary to make magnetic forces of these particles
opposite directed ones. This action is reflected in opposite directed
vectors ![]() and
and ![]() of magnetic moments
of the second proton and the second electron.
of magnetic moments
of the second proton and the second electron.
One more variant of
an arrangement of orthohydrogen molecule is shown in Fig. 53, b. The principle
of formation of this molecule is the same. Vectors of magnetic moments of the
electrons and the protons are directed in such a way that if electric forces
bring the particles nearer each other, magnetic forces should move away them
from each other. As a result, an equilibrium is established between them.
Stability of structure formed in such a way depends on binding energies between
its elements. As magnetic movements of the electrons are by a factor of ![]() greater than magnetic
moments of the protons ,electromagnetic forces of the first structure (Fig. 53,
a) keep its elements together stronger than in the structure shown in Fig. 53,
b, that’s why there is every reason to believe that the first structure of orthohydrogen
is more stable than the second one.
greater than magnetic
moments of the protons ,electromagnetic forces of the first structure (Fig. 53,
a) keep its elements together stronger than in the structure shown in Fig. 53,
b, that’s why there is every reason to believe that the first structure of orthohydrogen
is more stable than the second one.
Let us retrace
logical actions of the Nature during the formation of a molecule of parahydrogen
(Fig. 53, c). The logic of bond formation between the first electron and the
first proton remains the same. The forces of mutual attraction of the first
electron and the second proton are balanced by their opposite directed magnetic
forces.
It is easy to see
that the distances between the second proton and the electrons are less than
between the first electron and the second one; it means that electrostatic
forces of attraction of these electrons to the second proton will be greater
than electrostatic forces of repulsion acting between the first electron and
the second electron. Electrostatic forces of mutual attraction of the first electron
and the second proton are balanced by opposite directed magnetic forces. As
they are by a factor ![]() of greater in the
electrons than in the protons, vector
of greater in the
electrons than in the protons, vector ![]() of magnetic moment of
the second electron should be directed opposite to magnetic moment vector as it
is shown in Fig. 53, c.
of magnetic moment of
the second electron should be directed opposite to magnetic moment vector as it
is shown in Fig. 53, c.
It is high time to
analyze the existing notions concerning the chemical bond between atoms in the
molecules. They are described by several theories [36], [37], [38], [42].
Ion theory of bond
describes the bonds established between unlike charged ions. On these grounds
the bond between the first proton and the first electron as well as between the
second electron and the second proton in the molecules of orthohydrogen (Fig.
53, a) is considered to be an ion bond.
In accordance with
the covalent bond theory, it is formed by two non-coupled electrons of tow
atoms. Such bond can be observed between the first electron and the second one
of the orthohydrogen molecule (Fig. 53, a). The reason why this bond has been
called “covalent bond” is not clear for us, we’ll call the bond between the
electrons simply the electron bond, between the protons – the proton bond, and
the bond between the electron and the proton will be called the electron and
proton bond.
The hydrogen bond
theory describes chemical bonds realized by the hydrogen atom. The diagram of
the hydrogen atom (Fig. 50) shows that the hydrogen atom is an ideal link
between the atoms. This bond is formed both by Coulomb’s forces of the proton
and the electron and their magnetic forces.
It is known that
there is a phenomenon of electron capture by the proton and neutron formation
with the emission of the neutrino as the modern physicists think. Let us
consider the realization of this
phenomenon on the examples of the formation of the structures of the
atom and the hydrogen molecule. It is clear that the situation is possible when
vectors of magnetic moments (Figs 50, 51) of the proton and the electron
coincide. The electrostatic and magnetic forces will attract the electron and
the proton to each other, and the proton will absorb the electron. In order
that the proton becomes the neutron, it should absorb more than two electrons.
We have already noted that this process is realized during plasma electrolysis
of water as the Japanese scientists T. Ohmori and T. Mizuno have found out
[51]. The remainder of the third electron is called the neutrino by modern
physicists and chemists. As it has no charge, it is an evasive particle. We
have the possibility to suppose (i.e. to formulate another hypothesis) that a
part of the third electron is not absorbed by the proton, it dissipates as a
substance being called the ether [84].
10.4. Structure of
the Helium Nucleus and Atom
As it is known, the
helium atom has two electrons. We have already described the method of
determination of binding energy ![]() of the first electron
with the atomic nucleus, which corresponds to its first energy level. It is
equal to
of the first electron
with the atomic nucleus, which corresponds to its first energy level. It is
equal to ![]() =13.48 eV. Taking into consideration of ionization of this
electron
=13.48 eV. Taking into consideration of ionization of this
electron ![]() =24.587 eV and using spectroscopy law (212), we’ll get the
necessary data (Table 30).
=24.587 eV and using spectroscopy law (212), we’ll get the
necessary data (Table 30).
Table 30. Spectrum
of the first electron of the helium atom
|
Volume |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
21.22 |
23.09 |
23.74 |
24.04 |
24.21 |
|
|
eV |
21.22 |
23.09 |
23.74 |
24.05 |
24.21 |
|
|
eV |
3.37 |
1.50 |
0.84 |
0.54 |
0.37 |
Thus, if the
electron of the hydrogen atom interacting with the nucleus is at a distance,
which 100fold exceeds the size of the electron itself , it is interesting to
know the first electron of the helium atom interacts with the nucleus.
The reply to this
question is given by binding energy (3.37 eV) of the first electron with the
nucleus when it is on the second energy level (Table 30). In its quantity, this
energy resembles binding energy (3.40 eV) of the electron of the hydrogen atom
with the nucleus , which consists of one proton only when it is on the second
energy level (Table 29). It is clear that at such binding energy with the
nucleus the first electron cannot interact with two protons of the nucleus
simultaneously as the second electron of the helium atom does having binding
energy with the nucleus corresponding to the first energy level, which is equal
to 13.6×4=54.40 eV. It
appears from this that the first electron of the helium atom interacts only
with one proton of its nucleus. It is confirmed by the structure of the nucleus
of the helium atom (Fig. 22). Both protons
of the nucleus are arranged at two ends of the nucleus with linear
structure. Each electron interacts with its own proton (Fig. 54) [109].
Let us recollect
the spectroscopy analysis results, from which it is clear that all electrons
lack orbital motion energy and, consequently, the orbital motion itself. The
electron in the atom has only rotational energy relatively its axis, it being
the main unexpected result. It makes us think that the electron interacts with
the nucleus as a bar magnet, i.e. with its axis of rotation. Thus, the fact of
interaction of the first electron of the helium atom by the axis of rotation
with its nucleus from the spectroscopy law and is confirmed by a value of
binding energy (3.37 eV) with the nucleus when it is on the second energy
level.
1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() N
N
2
Fig. 54. Model of
the nucleus and the atom of helium: N is the nucleus of the atom, 1,2 are the
numbers of the electrons
It is necessary to
explain the notion “axis of interaction”. It is an imaginary line, which passes
through the magnetic poles of the electron or the proton. It connects
geometrical centers of the proton or the electron or two electrons when they
interact. Magnetic forces act along this line. They provide interaction of
these particles and together with Coulomb forces form the conditions for
stability of such formation.
When determining
the diagram of interaction of the second electron with the nucleus of the
helium atom one should take into account that magnetic moment of the helium
atom is equal to zero. It means that vectors of magnetic moments and vectors of
their angular moment are directed along one straight line in opposite
directions. The models of the helium atom with series of energy transitions of
the first electron is such as it is given in Fig. 55, c.
It is high time to
speak about the notion “orbital motion of electron”. Now this notion does not
reflect the essence, which is understood, that’s why it is necessary to introduce
a new notion, which should reflect the process of the discovered motion of the
electron in the atom more exactly.
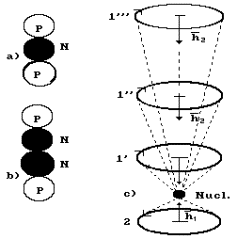
Fig. 55. Model of
the helium nucleus and the atom with energy transitions of the first electron:
a) diagram of the model of the isotope nucleus of the helium atom; b) diagram
of the model of the atomic nucleus of the helium atom; c) model of the atom:
1,2 are the numbers of the electrons; N is the atomic nucleus; 1’, 1’’, 1’” are
the energy levels of the first electron.
Let us recollect
that the chemists embarrassed by the fact that Schroedinger’s equation does not
give the opportunity to determine the exact position of the electron in the
atom and specifies probability, with which it is possible to determine the
position of the electron in this or that field of the atom, have decided to
substitute the notion “orbital” for “orbit” implying something uncertain [2].
Now we see (Fig.
55, c) that during absorption of the photon the electron moves relatively to
the nucleus along its axis of rotation, i.e. axis of symmetry, passing from one
energy level to another one. That’s why in the future we’ll not use the notion
“orbit”, we’ll use the notion “energy level”, or simply “level”. As the axis of
rotation of the electron during the interaction with the nucleus can deviate,
i.e. it can make precession motion, it is possible to call the movement of the
electron in the atom a precession one.
Let us consider the
electron charge. It is known that free electrons have one and the same charge.
The question arises: is this charge changed during energy transitions of the
electron in the atom? There is every reason to believe that it is changed. Let
us pay attention to the interaction of the first electron and the second
electron in the helium atom. Magnetic force repulsing the second electron from
the nucleus, is directed along the axis, which connects their centers, and the
electric forces, which exist between the electrons, bring them closer to each
other. Regularity of the change of these forces determines regularity of the
change of binding energy (213) of the electrons with the nucleus.
A very important
and interesting moment has come. As each electron of the helium atom interacts only with
its proton, their binding energies with each proton should be equal. But the experiment
gives another result. Let us copy out binding energies of the electron of the
hydrogen atom with the proton, which correspond to n energy levels, from Table
27 and binding energies of the second electron of the helium atom with its
nucleus from Table 10. Let us copy out binding energies with the atomic nucleus
of the first electron of the helium atom (Tabl. 13) and put everything in Table
31.
As it is clear, the
electron of the hydrogen atom ![]() and the first
electron
and the first
electron ![]() of the helium atom
have practically equal binding energies with the atomic nuclei at the
corresponding energy levels. Binding energy of the second electron
of the helium atom
have practically equal binding energies with the atomic nuclei at the
corresponding energy levels. Binding energy of the second electron ![]() of the
helium atom with its nucleus corresponding to the first energy level is
fourfold greater than the corresponding binding energy of the hydrogen atom,
that’s why all other values of binding energies of the electron, which are
equal to the corresponding binding energies of the first electron of the helium
atom and the electron of the hydrogen atom, are shifted.
of the
helium atom with its nucleus corresponding to the first energy level is
fourfold greater than the corresponding binding energy of the hydrogen atom,
that’s why all other values of binding energies of the electron, which are
equal to the corresponding binding energies of the first electron of the helium
atom and the electron of the hydrogen atom, are shifted.
Table 31. Binding
energies ![]() of the electron of
the hydrogen atom
of the electron of
the hydrogen atom ![]() and the first
and the first ![]() and the
second
and the
second ![]() of the
electrons of the helium atom He with the nuclei
of the
electrons of the helium atom He with the nuclei
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
13.6 |
3.40 |
1.51 |
0.85 |
0.54 |
0.38 |
0.28 |
0.21 |
0.17 |
|
|
- |
3.37 |
1.50 |
0.85 |
0.55 |
0.38 |
0.28 |
0.22 |
0.17 |
|
|
54.4 |
13.6 |
6.04 |
3.40 |
2.18 |
1.51 |
1.10 |
0.85 |
0.67 |
Let us pay
attention to the fact that within the framework of the permissible error
binding energies of the electrons of the helium atom (Table 31) corresponding
to the first energy level (n=1) are calculated according to the formula
![]() (247)
(247)
where ![]() is ionization energy
of the hydrogen atom, l is the number
of the electron in the atom corresponding to the number of the potential of its
ionization.
is ionization energy
of the hydrogen atom, l is the number
of the electron in the atom corresponding to the number of the potential of its
ionization.
Then the formula
for the calculation of binding energy of any electron of the helium atom
corresponding to any energy level will be as follows
![]() (248)
(248)
The coincidence of
the calculation results according to this formula with the experimental results
given in Table 31 proves correctness of the directions of the investigations.
When binding energy
of the second electron of the helium atom with the nucleus at the moment of its
stay on the third energy level is determined, the formula (248) will be written
in such a way:
![]() . (249)
. (249)
A question arises: why does each electron in the helium
atom interacts independently from each other with separate protons of the
atomic nucleus, and binding energies with the nucleus are different? The answer
will be as follows.
In reality when
both electrons are in the atom, and each of them interacts with its proton in
the nucleus, their binding energies with the nucleus are similar or almost
similar. When one electron is removed from the atom, the remaining electron
(the second electron) begins to interact with two protons of the nucleus, not
with one. Force ![]() of interaction between
the electron and the nucleus, which has two protons, will be written in the
following way:
of interaction between
the electron and the nucleus, which has two protons, will be written in the
following way:
![]() . (250)
. (250)
If we multiply the right part
by radius ![]() , which determines the distance between the electron and the
atomic nucleus, we’ll get the value of binding energy of the second electron
with the nucleus of helium atom.
, which determines the distance between the electron and the
atomic nucleus, we’ll get the value of binding energy of the second electron
with the nucleus of helium atom.
![]() . (251)
. (251)
It appears from
this that if the first electron of the helium atom returns to the atom, binding
energy of the nucleus of the second electron will be reduced and will be equal
to binding energy with the same nucleus of the first electron of the helium
atom.
This conclusion is
very important for chemistry. Both electrons of the helium atom have equal
probability of formation of the connections with the electrons of other atoms,
because they have equal binding energies with the nucleus on all energy levels.
Later on we’ll see the same regularity of formation of binding energies with
the atoms of the symmetrical structure of the nuclei.
10.5. Structure of
the Lithium Atom
We have already
shown that the majority of the atomic nuclei of lithium have 4 neutrons and
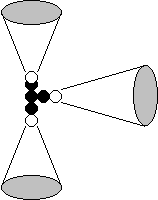
three protons (Fig. 23, a). All the protons have free magnetic poles for the
connection with the magnetic poles of the electrons when an atom is formed
(Fig. 56).
The connection is
established by means of interaction of the unlike electric fields of the
protons and the electrons, which bring them close to each other, and the like
magnetic poles, which restrict this approach. It comes out that each electron
interacts only with one proton of the atomic nucleus (Fig. 56).
The analysis of the
diagram of Fig. 56 shows that the electrons, which are arranged symmetrically,
will have similar binding energies with the nucleus. The electron, which is
arranged to the right of the nucleus, will be influenced by electrostatic
forces of repulsion of two other electrons, that’s why it will be situated
farther from the nucleus, and its binding energy with the nucleus will be the
smallest one. That’s why we confirm that first number to this electron.
2
1
N
3
Fig. 56. Diagram of
the models of the nucleus and the atom of lithium: N is the atomic nucleus;
1,2,3 are the numbers of the electrons
Let’s write binding
energies of the first electron of the lithium atom with its nucleus out of
Table 15 and of the second one out of Table 14. We’ll take binding energies
with the nucleus of the lithium atom of the third electron out of Table 8. Let us make a consolidated Table of binding
energies of the electrons of the lithium atoms with its nucleus (Table 32).
Table 32. Binding
energies ![]() of the electron of
the hydrogen atom
of the electron of
the hydrogen atom ![]() and the first, the second
and the third electrons of the lithium atom Li with the nucleus
and the first, the second
and the third electrons of the lithium atom Li with the nucleus
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
13.6 |
3.40 |
1.51 |
0.85 |
0.54 |
0.38 |
0.28 |
0.21 |
0.17 |
|
1 |
14.06 |
3.51 |
1.56 |
0.88 |
0.56 |
0.39 |
0.29 |
0.22 |
0.17 |
|
2 |
54.16 |
13.54 |
6.02 |
3.38 |
2.17 |
1.50 |
1.10 |
0.85 |
0.67 |
|
3 |
122.5 |
30.6 |
13.6 |
7.65 |
4.90 |
3.40 |
2.50 |
1.91 |
1.51 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
0.14 |
0.11 |
0.09 |
0.08 |
0.07 |
0.06 |
0.05 |
0.05 |
0.04 |
|
1 |
0.14 |
0.12 |
0.10 |
0.08 |
0.06 |
0.06 |
0.05 |
0.05 |
0.04 |
|
2 |
0.54 |
0.45 |
0.38 |
0.32 |
0.28 |
0.24 |
0.21 |
0.19 |
0.17 |
|
3 |
1.23 |
1.01 |
0.85 |
0.72 |
0.63 |
0.54 |
0.48 |
0.42 |
0.38 |
If we analyze Table
32, we see proximity of binding energies of the electron of the hydrogen atom
and the first electron of the lithium atom on the first, the second and the
third energy levels and almost complete coincidence on all the rest ones. It is
one of the evidences of the fact that the first electron of the lithium atom
interacts with one proton of the nucleus of its atom.
It is not difficult
to see that if one (the third) electron remains in the lithium atom, it will begin
to interact with three protons at once, and its binding energy with the
nucleus, which corresponds to the first energy level, will be determined
according to the formula (248).
![]() ,
(252)
,
(252)
It coincides with
the values of this energy in Table 32 and confirms our hypothesis in relation
to the fact that if one electron remains in the atom, it interacts
simultaneously with all protons of the nucleus.
Let us calculate
binding energy of the third electron of the lithium atom with the nucleus
according to the formula (248) when it is on the fifth energy level.
![]() (253)
(253)
As it is clear,
this value matches similar binding energy of the third electron of the lithium
atom with the nucleus when it is on the fifth energy level (Table 32). As the
lithium atom with one electron is the hydrogen-like atom, let us calculate
binding energy of the second electron of this atom with the nucleus to be
convinced when it is on the seventh energy level.
![]() .
(254)
.
(254)
This result matches
binding energy of the second electron of the lithium atom when it is on the
seventh energy level (Table 32). If we managed to measure binding energy of two
remaining electrons of the lithium atom with the nucleus without removal of the
first electron from it, it would appear that all three electrons have equal
binding energies with the nucleus. But it is hardly possible to carry out such
an experiment at this stage of scientific research. But we have already given a
hypothetical explanation of this phenomenon.
The coincidence of
the calculation results according to the formulas (247) and (248) with the
experimental results given in Table 32 proves viability of this explanation.
It is easy to imagine that various
values of binding energies of various electrons of the lithium atom (Table 32),
which correspond to the first energy level (n=1) are obtained due to the fact
that after removal of the first electron from the atom the released proton
begins to interact with the second electron increasing its binding energy to a
value, which is near to binding energy of the second electron of the helium
atom (Table 32).
When the second
electron is removed from the atom, two free protons are in the nucleus, which
begin to interact with the remaining third electron increasing its binding
energy with the nucleus ![]() fold.
fold.
If we begin to
return consequently all electrons to the atom, the number of the protons, which
have interacted earlier with one electron, begins to be reduced. Binding energy
of this electron will be reduced to the value, which is approximately equal to
binding energy with the electron nucleus of the hydrogen atom.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index