<<
Back to Kanarev's Physchemistry Book Index
9. MODELS OF ATOMIC NUCLEI OF CHEMICAL ELEMENTS
9.1. General Data on Atomic Nuclei
If the
electromagnetic models of the proton and the neutron were known, the task of
the determination of the structure of the atomic nuclei of chemical elements
would be simplified significantly. But they are not available. That’s why we
should base our assertions only on the experimental facts and deductions, which
originate from the results of theoretical investigations [27], [118], [121],
[138], [154], [167], [170].
The first and the
most important result of our investigations, which belongs to the atomic
nucleus, is the lack of orbital movement of the electron in the atom. The
electrons interact with the atomic nuclei with their axes of rotation. It is
possible if the protons of the nucleus are arranged on its surface [18], [26],
[109].
Thus, in order to
provide the interaction of each electron with the nucleus, it is necessary to
arrange the protons on the surface of the nucleus. The same charges of the
protons exclude the structure of the nucleus, in which the protons could touch
each other. The nature builds the nucleus in such a way that a neutron should
be between the protons. As the last requirement is difficult to be met when there are many protons in the nucleus, additional
neutrons are attracted. That’s why the nuclei of almost all chemical elements
contain more neutrons than protons. When the number of the protons and the
neutrons in the nucleus is increased, the share of “extra” neutrons is
increased. It is clear, because it is impossible to get geometrical symmetry of
the nucleus, in which the neutrons should be present between the protons [27],
[130].
It seems that the
neutrons are penetrable for magnetic fields of the protons and unpenetrable or
weakly penetrable for their electrical fields. Screening the like electrical
fields of the protons, the neutrons create the conditions when the magnetic
poles of the protons interact with the unlike magnetic poles of the neutrons
[121].
The electron and
the proton have the charges and the magnetic moments. We have already found
that the magnetic field of the electron is similar to the magnetic field of a
bar cylindrical magnet. One can suppose that the charge of the proton helps to
form the same magnetic field as the field of the electron, i.e. the structure
of the magnetic field of the proton is similar to the structure of the magnetic
field of the bar cylindrical magnet. Let us call such magnetic field a simple
magnetic field [121].
The neutron has
magnetic moment as well and, consequently, magnetic field. But we know nothing
about the structure of its magnetic field. If it is similar to magnetic field
of the bar cylindrical magnet, the proton and the neutron are connected as the
bar magnets, and the structure of the nuclei should be linear. If the neutron
has a compound magnetic field, which consists of several magnetic poles, the
construction of the atomic nuclei with more complicated space configuration is
possible [121].
That’s why the
determination of the structure of the magnetic field of the neutron is one of
the priority tasks in our search. We have already called the magnetic field of
the proton, which is similar to the magnetic field of the bar cylindrical
magnet, a simple symmetrical magnetic field. There is every reason to believe
that the magnetic field of the neutron has more complicated configuration;
that’s why let us call it a compound magnetic field [121].
As the nuclei of
all chemical elements consist of the positively charged protons and uncharged
neutrons, it is necessary to systematize the information concerning the main
characteristics of these elementary particles in order to detail the
principles, which control the formation of the nuclei of chemical elements.
9.2. On
Model of the Proton
It is known that rest
mass of the proton is ![]() Electrical charge of the proton is positive and is equal to the
negative charge of the electron
Electrical charge of the proton is positive and is equal to the
negative charge of the electron ![]() . Magnetic moment of the proton is equal to
. Magnetic moment of the proton is equal to ![]() Electromagnetic structure of the
proton is unknown. If we suppose that it (as the electron) has the form of a
torus, radius
Electromagnetic structure of the
proton is unknown. If we suppose that it (as the electron) has the form of a
torus, radius ![]() of this torus is as
follows [109]
of this torus is as
follows [109]
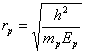
![]() (230)
(230)
where ![]() is mass of the
proton,
is mass of the
proton, ![]() is the photon energy
of the proton.
is the photon energy
of the proton.
Thus, radius of the proton is by three orders of magnitude
less than radius of the electron. Spin of the proton (as spin of the electron)
is equal to Planck’s constant. Vectors of these spins are directed along the
axes of their rotation. The directions of spins both of the proton and the
electron coincide with the directions of vectors of their magnetic moments
[70]. It appears from the formula (149), which connects Planck’s constant and
magnetic moment of electron ![]() . Let us present it in the following way
. Let us present it in the following way
![]() (231)
(231)
In modern physics, vectors ![]() and
and ![]() are considered to be
opposite directional. It is reasoned by the fact that the charge of the electron
are considered to be
opposite directional. It is reasoned by the fact that the charge of the electron
![]() in the formula (149)
is negative. Rather a strange reason. The nature gives vector properties to
values
in the formula (149)
is negative. Rather a strange reason. The nature gives vector properties to
values ![]() and
and ![]() . Physicists themselves have given a negative sign to the
charge of the electron
. Physicists themselves have given a negative sign to the
charge of the electron ![]() . It is conventional agreement, not the law of the nature! In
formula (149), the charge of the electron
. It is conventional agreement, not the law of the nature! In
formula (149), the charge of the electron ![]() is a scalar value,
and we have no reason to write it as follows [109]
is a scalar value,
and we have no reason to write it as follows [109]
![]() (232)
(232)
Let alone logic of modern physicists; we’d like to consider the formula
(231), from which it appears that vectors ![]() and
and ![]() are directed to one
side.
are directed to one
side.
Magnetic field
strength in the vicinity of geometrical centre of the toroidal model of the
proton is considerably greater than the same magnetic field strength of the
electron. If we assume that the proton is a torus as well, we’ll get magnetic
field strength ![]() in the vicinity of
the centre of symmetry of the proton using magnetic moment of the proton
in the vicinity of
the centre of symmetry of the proton using magnetic moment of the proton ![]() and its photon energy
and its photon energy
![]()
![]() [109]
[109]
![]() (233)
(233)
This is colossal magnetic field strength in the centre of symmetry of the proton. Outside this centre, it is decreased
quickly. Along the axis of rotation of the proton this decrease is inversely
proportional to cube of the distance from its geometrical centre [24]. Such
large magnetic field strength generates corresponding large magnetic forces. If
magnetic field of the proton is similar to magnetic field of the bar
cylindrical magnet, unlike magnetic poles will juxtapose the protons and the
neutrons.
If we imagine the proton in the form
of a sphere with radius ![]() ,
Coulomb force will act during the direct contact of two protons between them
,
Coulomb force will act during the direct contact of two protons between them
![]() (234)
(234)
For the sake of comparison, let us calculate gravitational force,
which exists between the protons in this case
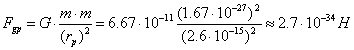 (235)
(235)
The results of these calculations prove that
during formation of the atomic nuclei electrostatic forces and magnetic ones,
not gravitational forces, play a decisive role. They form the atomic nuclei.
In order to get a
clear understanding on the proton model, we’d like to note that in the first
approximation it is a rotating torus, which can be presented in the form of a
geometrical figure having a form of an apple with the magnetic field lines
passing along the axis of the apple and closing on each other. Electrical field
lines are directed perpendicular to the magnetic filed lines or perpendicular
to toroidal surface. Such model has almost spherical electrical field and two
magnetic poles: the north pole and the south one. The poles are formed at
different ends of axis of rotation of torus. Let us call the described
structure of magnetic field a simple structure, and the unknown structure of
electromagnetic field of the neutron a compound structure [121].
9.3. On
Model of the Neutron
It is known that
rest mass of the neutron is ![]() . The difference between mass of the neutron and the proton is equal to
. The difference between mass of the neutron and the proton is equal to ![]() [109]. Thus, mass of the neutron
is larger than mass of the proton by
[109]. Thus, mass of the neutron
is larger than mass of the proton by ![]() masses of the electron. It
appears from this that in order a proton becomes a neutron, it should capture
2.531 electrons. As there are no electrons with fractional mass, the proton
should absorb the whole number of the electrons. If it absorbs three electrons,
and its mass is increased only by 2.531 masses of the electron, a question
arises: what will become of the remainder of mass of the electron
masses of the electron. It
appears from this that in order a proton becomes a neutron, it should capture
2.531 electrons. As there are no electrons with fractional mass, the proton
should absorb the whole number of the electrons. If it absorbs three electrons,
and its mass is increased only by 2.531 masses of the electron, a question
arises: what will become of the remainder of mass of the electron ![]() ? Modern physics explains the disturbed balance of masses in this
process simply: a neutrino is born, which has no charge; that’s why it is very
difficult to register the birth of this particle as it is assumed in modern
physics. The neutron has magnetic field. Its magnetic moment is estimated by
the value
? Modern physics explains the disturbed balance of masses in this
process simply: a neutrino is born, which has no charge; that’s why it is very
difficult to register the birth of this particle as it is assumed in modern
physics. The neutron has magnetic field. Its magnetic moment is estimated by
the value ![]() [1].
[1].
The neutron has no
charge. As the mass of the neutron differs insignificantly from the mass of the
proton, one can suppose that they have similar geometrical dimensions. One can
suppose that the neutron radius is almost the same as the proton radius or is a
bit larger than the proton radius.
As we try to find
the principle, by which the nature is guided when it forms the atomic nuclei,
our information concerning the models of the proton and neutron shows that
these particles, which control the formation of the atomic nuclei, have the
following properties: the charge and magnetic moment of the proton as well as
magnetic moment of the neutron and the lack of charge. Availability of magnetic
moments with these particles gives us the reason to imagine that they have
magnetic poles [121].
Magnetic forces of
unlike poles of magnetic fields of the proton and the neutron are the only
forces, which can connect these particles with each other. Electrostatic forces
of the protons are the only forces, which limit the approach of the protons in
the nucleus.
Nevertheless, the
experiments have revealed the existence of nuclear forces connecting the
protons and the neutrons in the atomic nuclei. The value of these forces is by
a factor of 102 of electrostatic repulsive forces of the protons.
The forces generating such interaction are called nuclei forces. Their nature
remains unknown.
If we take into
consideration large magnetic field strength near the centre of symmetry of the
proton (233) and suppose that it is the same with the neutron, there is every
reason to believe that magnetic forces of the proton and the neutron acting at
the distances near to their geometrical centres are the forces, which have been
called the nuclei ones [121].
Thus, we have a
possibility to suppose that the nuclei forces are the magnetic forces acting at
the smallest distances between the centres of masses of the protons and the
neutrons. First of all, let us consider the spherical models of the protons and
the neutrons with the magnetic fields, which are similar to symmetrical
magnetic fields of the bar cylindrical magnets and the reasons of existence of
six-pole magnetic with the neutron.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index