<<
Kanarev´s Page In Russian >>
Published 19.05.2004
NEW FUNDAMENTAL CONSTANT
Ph.M. Kanarev
E-mail: kanphil@mail.ru
Abstract. The
constant h/C=m×l2×v/l×v=m×l=const has
been known for a long time. As it was impossible to coordinate a strange
dimensionality of this constant kg×m with physical
sense hidden in product of its mathematical symbols m and l, it was not included in the number of
fundamental constants. Now, this task has been solved. The constant m×l=const contains a law, which managers
localization of the photon in space, that's why we have called it a photon
localization constant.
Keywords. Photon, electron, spectrum, mass, wavelength, frequency, electromagnetic emission scale
It is known that velocity of light C=l×v=const and Planck’s constant h=ml2v=const are
the main fundamental constants, which take part in the photon behaviour
description.
We have already shown that
congruence of photon wavelengths l to radii r of their rotation is the first condition of photon localization
in space [1]
![]() . (1)
. (1)
Taking it into consideration, the
formula for the definition of C photon velocity will be written in the
following way
![]() . (2)
. (2)
If there is no condition l = r, the
constant h=ml2v=const having dimensionality of moment of momentum or
angular momentum or angular impulse kg×m2/s has no physical sense. l wavelength in Planck’s constant expression
shows that this constant describes a wave process. The above-mentioned
dimensionalities mean a rotation process described by this constant. This
contradiction in terms disappears only when l=r. In this case Planck’s
constant
![]() (3)
(3)
gets clear physical sense: moment of
momentum, or angular momentum, or angular impulse of the ring (Fig. 1) [1].
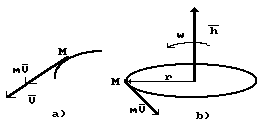
Fig. 1. Diagram for definition of the notions:
a) momentum ![]() of material particle,
b) angular momentum `h of the
ring
of material particle,
b) angular momentum `h of the
ring
One more constant originates from the
expressions (2) and (3)
![]() .
(4)
.
(4)
Its dimensionality is M×L=kg×m. In SI
system, there is no value with such dimensionality; that’s why it becomes
necessary to introduce a name of this constant [2]. It appears from the new
constant k0=mr=const that
the photon ring radius r is reduced
with the increase of mass m of the photon and vice verse. As l=r, it means that if the photon is similar to
the ring, product of mass m of the photon by ring radius r is constant. It is clear that it is the photon localization law
in space. We have every reason to call value k0=mr=const a photon localization constant. In SI
system, it is equal to [1]
![]() . (5)
. (5)
A question arises: what
electromagnetic structure should belong to the photon in order to provide such
remarkable combination of its parameters m, r and v that are changed in such
wide range in such a way that constancy of three constants h, C and k0
is provided at once?
It appears from Planck’s constant h=mr×rv=const that the photon has a form of the rotating
ring (Fig. 2, a) that moves with constant speed C=lv=rv=const.
The new constant k0=mr=const determines
the law of variation of mass m of the
photon and radius r of its ring. It
runs as follows: when the photon mass m
is increased, its radius r is
proportionally reduced and vice verse.
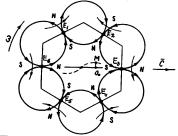
It appears from equality l=r that the
ring is divided into six parts by the chords (Fig. 2,b). We have every reason
to suppose that the photon consists of six electromagnetic fields, each of them
having center of mass E (Fig. 2, c).
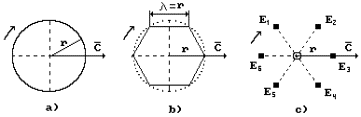
Fig. 2. To photon structure revelation
As the photon has mass and
electromagnetic nature, we have the only possibility: to think that the photon
mass is formed by its six electromagnetic fields. Availability of gyrating
masses predetermines availability of centrifugal forces of inertia, and
electromagnetic nature of the photon predetermines availability of
electromagnetic forces. Continuity of three constants h, C and k0 should
be provided by equation between Newtonian forces influencing the centres of
mass E of these fields and
electromagnetic forces generated by the moving electromagnetic fields. It
appears from this that the photon localization in space is provided by the
electromagnetic and centrifugal forces of inertia balancing each other.
As the centrifugal forces of inertia
are directed radially from the centre of rotation, the magnetic component of
electromagnetic forces should be directed radially as well, but to the centre
of rotation. It is possible if the magnetic fields are similar to the magnetic
fields of the bar magnets arranged radially and directed towards each other by
their unlike magnetic poles [1].
The diagram of the electromagnetic
model of the photon, which is shown in Fig. 3, a, appears from this. The same model
simulated by Walter Krauser, the German physicist, with the help of the
constant magnets is given in Fig. 3, b [3].
|
a) |
b) |
Fig. 3. Diagrams of the electromagnetic models
of the photon:
a) theoretical model, b) simulated model
As it is clear (Fig. 3), the model
of the photon consists of six magnetic fields closed with each other, which are
girded by the electric fields and are converted into electromagnetic fields
when the model moves. Magnetic fields of the photon are alike magnetic fields
of the bar magnets. These magnetic field vectors alternate in such a way that
in the opposite fields they are directed along one diameter in the same
direction compressing the photon. As the photon moves constantly, the magnetic
forces squeezing the photon are balanced by centrifugal forces of inertia
influencing the centres of mass E of
electromagnetic fields (Fig. 2, c) [1].
The model is complicated, but only
in this model the physical sense of all three constants k0, h and C is
realized in the following way.
It is known that when photon mass m
(energy) is increased, its wavelength (l=r) is decreased. This regularity originates from the photon
localization constant k0=mr=const.
As mr=const, m increase reduces r automatically.
It appears from the law of conservation of angular momentum h=mr2v=const as well. When
photon mass m is increased, density
of its electromagnetic fields is increased (Fig. 3); on this account,
electromagnetic forces compressing the photon are increased; these forces are
balanced always by the centrifugal forces of inertia influencing the centre of
mass of these fields. It results in a reduction of photon rotation radius r that is equal always to its wavelength
l. As radius r
in the expression of Planck’s constant is squared, photon oscillation frequency
v should be increased in order to
preserve continuity of Planck’s constant. Due to it, small change of photon
mass m automatically changes its
rotation radius r and frequency v in such a way that angular momentum
(Planck’s constant) remains the same. Thus, preserving its electromagnetic
structure the photons of all frequencies change mass, frequency and wavelength
in such a way that h=mr2v=const.
It means that the law of conservation of angular momentum governs this change
principle.
We get
the same clear answer to the following fundamental question: why do the photons of all frequencies move
in vacuum with similar velocity?
It is so, because the photon
localization law k0=mr=const
in space governs photon mass m and
its radius r. It appears from it that
when photon mass m is increased, its
radius r is decreased proportionally and vice verse. For continuity
conservation of Planck’s constant h=mr×rv=const by mr=const and r decrease, frequency v
should be increased proportionally. As a result, their product remains constant
and equal to C=lv=rv=const
[1].
We have already shown that from
photon model movement analysis (Fig. 3) all main mathematical relations
describing the photon behaviour are derived analytically, including Louis de Broglie’s wave equation and Schroedinger
equation [1]. The equation of motion of the centre of mass of the photon is as
follows:
![]() (6)
(6)
![]() (7)
(7)
where w=a×v=60°×v.
Velocity of the centre of mass of the photon is
changed according to dependence
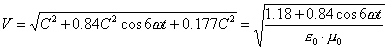 , (8)
, (8)
where e0, m0 are electrical constant and magnetic constant.
The diagram of velocity change (8)
of the centre of mass of the photon is shown in Fig. 4. As it is clear,
velocity of the centre of mass M of
the photon is changed in the wavelength interval or oscillation period in such
a way that its average value remains constant and equal to C [1].
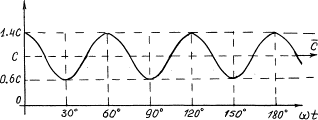
Fig. 4. Diagram of velocity change of the
centre of mass of the photon
Now it is necessary to find the
change borders of parameters m and r allocating the photon in space.
It should be noted that Maxwell’s
equation does not contain information concerning electromagnetic radiation
allocation is space (Table 1) [4].
It
is known that electromagnetic radiation is spread with velocity of light C»300000 km/s. Its wavelength l is
changed in the range of l»(107 ...10-18) m, and frequency v is changed
in the range of v»(101...1024), s-1. The whole electromagnetic scale is divided into ranges (Table 1) [1].
Table
1 Electromagnetic radiation
scale ranges
|
Ranges |
Wavelength, m |
Oscillation frequency, s-1 |
Energy, eV |
|
1. Low-
frequency range |
|
|
|
|
2.
Broadcast range |
|
|
|
|
3. Microwave
range |
|
|
|
|
4. Relic
range (max.) |
|
|
|
|
5.
Infrared range |
|
|
|
|
6. Light
range |
|
|
|
|
7.
Ultraviolet range |
|
|
|
|
8.
Roentgen range |
|
|
|
|
9. Gamma
range |
|
|
|
The new
constant k0=mr=const gives
the possibility to add the photon mass values corresponding to each range to
this Table (Table 2).
Table 2. Change ranges of wavelength l, mass m and energy E of
electromagnetic radiations
|
Ranges |
Wavelength, m |
Mass, kg |
Energy, eV |
|
1. Low- frequency range |
|
|
|
|
2. Broadcast range |
|
|
|
|
3. Microwave range |
|
|
|
|
4. Relic
range (max.) |
|
|
|
|
5. Infrared range |
|
|
|
|
6. Light range |
|
|
|
|
7. Ultraviolet range |
|
|
|
|
8. Roentgen range |
|
|
|
|
9. Gamma range |
|
|
|
As the electromagnetic radiation
structure is unknown, the photon corresponding to maximal wavelength l»3×108 m of this radiation (Table 1) should have the following mass
![]() . (9)
. (9)
Then the photon corresponding to the gamma
range will have mass
![]() (10)
(10)
Now it is clear that maximal
permeability of the gamma photon is provided by its minimal radius l»3×10-18 m and maximal mass m»0.7×10-24 kg. As far as the photon with maximal wavelength l»3×108 m and minimal mass m»0.7×10-50 kg is concerned, total uncertainty remains. It is difficult to
imagine a photon with radius r»3×108 m moving with velocity of light. Space area limited by radius r»3×108 m will be equal to S=pr2=3.14×3×108=9.42×1016 m2. The photon specific density will
be
![]() . (11)
. (11)
By such small photon mass density,
the formation of the Newtonian and electromagnetic forces is rather doubtful.
That’s why there should be a limit of maximal radius rmax and minimal mass mmin of the photon. Our next task is a search of this
limit.
Let us pay attention to a
significant experimental fact. Spectral line width can serve as an indirect
proof of the fact that the light photon size cannot exceed spectral line
thickness. As this line is formed by innumerable quantity of the photons,
actual size of the photon is significantly less that spectral line width. Two
bright spectral lines of the hydrogen atom are shown in Fig. 5.

Fig. 5. Spectral lines of the hydrogen atom
It is known that the photons forming the spectral lines emit electrons
during energy transitions in the atoms. It appears from this that they form
electromagnetic waves. How do they do it? Allan Holden’s hypothesis gives an answer
to this question. He presented electromagnetic wave structure in the following
way (Fig. 6) [5].
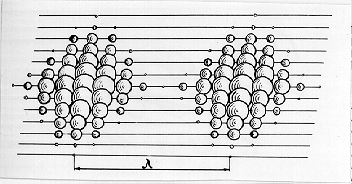
Fig. 6. Diagram of electromagnetic wave with
length l according to Allen Holden [5]
The diagram is remarkable for the fact
that an electromagnetic wave is formed by the pulses of single photons, which
are represented as the balls of different sizes by the author. The balls are
the photons. The distance between the pulses of the photons (balls) is equal to
wavelength of electromagnetic radiation. Wavelength of each separate photon is
considerably less. It determined the area of its allocation in space. If it is
so, a value of maximal radius rmax and consequently of minimal mass
mmin of the photon can be derived from the atom spectra analysis. In
Table 3, the hydrogen atom spectrum is given, including the 150th energy level.
Modern science does not know how many energy levels the hydrogen atom electron
and the electrons of other atoms have. That’s why we’ll try to find it out [1].
Table 3. Spectrum of the hydrogen atom
|
Energy
level number
|
Excitation
energy (eV) |
Binding
energy of the electron with the nucleus (eV) |
|||
|
1 |
-0.00000000000000075 |
13.59800000000000000 |
|||
|
2 |
10.19849999999999872 |
3.39950000000000000 |
|||
|
3 |
12.08711111111111168 |
1.51088888888888896 |
|||
|
4 |
12.74812500000000000 |
0.84987500000000000 |
|||
|
5 |
13.05408000000000000 |
0.54391999999999992 |
|||
|
6 |
13.22027777777777664 |
0.37772222222222224 |
|||
|
7 |
13.32048979591836672 |
0.27751020408163264 |
|||
|
8 |
13.38553125000000000 |
0.21246875000000000 |
|||
|
9 |
13.43012345679012352 |
0.16787654320987654 |
|||
|
10 |
13.46202000000000000 |
0.13597999999999998 |
|||
|
…. |
…. |
…. |
|||
|
100 |
13.59664020000000000 |
0.00135980000000000 |
|
||
|
101 |
13.59666699343201536 |
0.00133300656798353 |
|
||
|
102 |
13.59669300269127424 |
0.00130699730872741 |
|
||
|
103 |
13.59671825808275968 |
0.00128174191724008 |
|
||
|
104 |
13.59674278846153984 |
0.00125721153846154 |
|
||
|
105 |
13.59676662131519232 |
0.00123337868480726 |
|
||
|
106 |
13.59678978284086784 |
0.00121021715913136 |
|
||
|
107 |
13.59681229801729536 |
0.00118770198270591 |
|
||
|
108 |
13.59683419067215360 |
0.00116580932784636 |
|
||
|
109 |
13.59685548354515456 |
0.00114451645484387 |
|
||
|
110 |
13.59687619834710784 |
0.00112380165289256 |
|
||
|
…. |
…. |
…. |
|
||
|
148 |
13.59737920014609152 |
0.00062079985390796 |
|
||
|
149 |
13.59738750506733824 |
0.00061249493266069 |
|
||
|
150 |
13.59739564444444416 |
0.00060435555555556 |
|
||
What factor determines the limit energy level of the electron of the hydrogen atom? In order to find an answer to this question, let us pay attention to the relic range (Tables 1 and 2). This is a maximum of radiation intensity of the whole Universe. The wavelength of this radiation is nearly one millimetre [6], [7]. Regularity of change of this intensity (Fig. 7) resembles regularity of intensity of the perfect blackbody radiation. That’s why it has been assigned to cooling of the Universe since the day of its creation [6], [7].
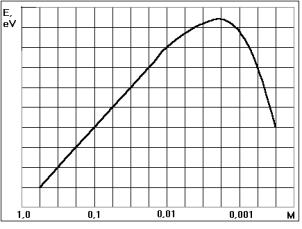
Fig. 7. Relic radiation intensity logarithm
dependence on the wavelength
One more hypothesis has appeared recently [1]. The relic radiation range corresponds to the limit of existence of the single photons. There are no single photons with the wave-length of more than the wave-length of the relic range. Here, maximum is formed due to the fact that all photons with the wavelength being less than the relic radiation wavelength lose their energy (mass) gradually in the process of their life interacting with the atoms and the molecules of the environment in accordance with Compton effect; they increase the wavelength (radius) and enter the relic range [1].
As it is clear (Tables 1 and 2), by l=r the
smallest photon is the gamma photon, and the largest photon is the infrared
photon of the relic range.
The lower limit of the photon radius
corresponding to the gamma photon does not stagger. In order to find the upper
limit of the photon radius, it is necessary to find the last energy level of
the electron of the hydrogen atom. Then it is necessary to subtract the photon
energy of the last but one energy level. If the energy difference being
obtained corresponds to the photon energy of the relic range, it will be a
valid proof that this range is the upper limit for the single photons. In
Tables 1 and 2, the photon corresponding to the maximal relic radiation has
energy E»1.2×10-3 eV.
Let us determine more exact value of
the photon energy, which wavelength is equal to the maximal wavelength (l=0.001 m) of the relic radiation (Fig. 7).
![]() (12)
(12)
As it is clear (Table 3), this
energy is similar to binding energy (0.00123337 eV) of the electron of the
hydrogen atom when it is on the 105th energy level. A binding energy value of
the electron of the hydrogen atom with the proton corresponding to the 105th
energy level (Table 3) can be obtained with the help of two methods.
The first method: to subtract excitation energy corresponding to the 105th energy level
(Table 3) (13.5967662 eV) from ionization energy (13.59800000 eV).
13.
598000000 eV-13.5967662 eV =0.0012338eV (13)
The second method: according to the formula determining the law of variation of binding
energy of the electron with the atomic nucleus
![]() (14)
(14)
Thus, we have got the result
originating from the experimental spectroscopy and confirming our hypothesis: the
relic range is the limit of existence of the large photons.
The evidence being obtained will be
strengthened if we find a photon energy value corresponding not to maximal
intensity of the relic range, but to the maximal wavelength lmax of this radiation (Fig. 7). For this purpose,
let us subtract excitation energy corresponding to the 104th energy level
(Table 3) from excitation energy of the 105th energy level. As a result, we’ll
have
13.596766621 -13.596742788 = 0.000024 eV. (15)
This energy corresponds to the maximal possible
wavelength of the photon.
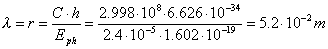 (16)
(16)
In Fig. 7, this length is to the left
of the maximal relic radiation, i.e. it corresponds not to the maximal
intensity of the relic range, but to the maximal wavelength lmax of this radiation (Fig. 7). If the relic range
of electromagnetic radiation corresponds to the maximal possible wavelength of
the photon being equal to 0.05 m, the electron of the hydrogen atom will emit
this photon during transition from the 105th energy level to the 104th one.
Thus, the maximal wavelength of the single photons corresponds to the relic range, and the minimal wavelength corresponds to the gamma range (Table 1). From the relic range to the gamma range, the photon wavelength is decreased by 15 orders, and frequency is increased similarly. As the photons of all ranges move with the same velocity C and form the electromagnetic radiation waves (Fig. 6), all ranges electromagnetic radiation velocity is the same [1].
Thus, the hypothesis being suggested
divides the electromagnetic radiation scale by two classes: the photon class
and the wave class. The photons are single electromagnetic formations emitted
by the atomic electrons. The aggregate of the photons emitted by the atomic
electrons forms a field that is called the electromagnetic field. It can be
continuous or pulsed – wave one (Fig.
6).
The photon model evokes many new
questions. More than 100 answers to such questions are published in the book
[8]. Here, we give some of them.
ANALYSIS OF EXPERIMENTAL
RESULTS
1. Why do the photons fail to exist in rest?
Because
the centre of photon masses M (Fig.
3) never coincides with its geometrical centre O0. This lack of
coincidence will create asymmetry between the electromagnetic fields of the
photon. This asymmetry does not allow it to be in rest. It is always in the
state of unstable equilibrium, which causes its movement.
2. Why do the photons
possess the properties of a wave and of a particle at the same time?
As
the electromagnetic fields are closed along the round contour, the photon
obtains the properties of a particle, and the oscillations of the centre of
masses M of this particle relative to the geometrical centre O0
impart the wave properties to it (Fig. 3). As the photon surface is not a
spherical one, but it has a complicated curvilinear form, interacting with the
objects, which form diffraction and interference pictures, they will be
distributed on the screen not at random, but in accordance with the surface
form and the interaction laws, which result from this.
3. Why are the photons
polarized?
They
rotate in one plane, and the centrifugal forces of inertia influencing the
centres of the masses of electromagnetic fields of the photon increase their
radial dimensions and reduce the dimensions, which are perpendicular to the
plane of rotation. Due to it, the photons acquire a form, which is different
from the spherical one and resemble the flat one.
4. Why do the photons
possess no charge?
They
consist of even quantity of direction different electrical and magnetic fields,
which make the total charge of the photon equal to zero.
5. What is the nature of the
radiowave range of the scale of electromagnetic radiation?
The
radiowave range of radiation is a flux of photons, and the modelled radiowave
is a flux of photon pulses (Fig. 6) of various density or frequency.
6. Why is the propagation
distance of a surface radio wave is increased with the increase of its length?
Due
to the increase of the length of the radiowave, the number of the photons,
which form this wavelength (Fig. 6), is increased, and the possibility of delivery
of information by such wave is increased, despite of the fact that a part of
the photons is disseminated by the environment, and a part of them is absorbed.
If the wavelength is reduced, the number of the photons, which carry it, is
reduced, and the possibility of delivery of information to the receiver is
reduced.
7. In which way does a radiowave with the length measured in kilometres
transmit the information to an aerial of the receiver, which dimensions can be
only several centimetres or even less?
Information transmission by the
radiowave with the length measured in kilometres to the aerial of the receiver,
which dimensions are by several orders less than the radiowave length, is
possible due to the fact that this wave is carried by the aggregate of single
photons. That’s why in order to excite the electrons of the aerial of the
receiver in a specified succession it is enough that several photons from (Fig.
6) this aggregate (wave) come to it.
8. Why does the relic radiation have the largest intensity in the
millimetre range?
In this range, the wavelength of the
infrared photon, which is the largest in size, but the smallest in mass, is
situated, and all photons lose their mass gradually in the process of their
life and repeated collisions and regenerate into the infrared photons with the
least mass (energy). The wavelength of these photons is in the millimetre
range. Apparently, the relic radiation is a radiation of the obsolete photons.
CONCLUSION
The new fundamental constant k0=mr=const plays the main
role in the formation of the electromagnetic structure of the photon. Its
physical sense together with the physical sense of Planck’s constant `h=ml2v=mr2v=const and the mathematical model
determining velocity of the photon C=l×v=r×v=const has enough
information for a disclosure of the electromagnetic structure of the photon.
REFERENCES
1. Ph.M. Kanarev. The Foundations of Physchemistry of
Microworld. The fifth edition. Krasnodar, 2004. 400
pages.
2. G.D. Burdun. SI
unit international system manual. Standards publishing house. M. 1977.
3. Walter Kranzer. So interesant Physic. Berlin. 1990.
4. V.V. Nikolsky,
T.I. Nikolskaya. Electrodynamics and Wave Propagation. M.:
Nauka. 1989.
5. Allan Holden. What is FTT. M. “Mir”, 1979
6. V.S. Edelman. Near absolute zero. M. “Nauka”, 1983. 174 pages
7. Ya.A. Smorodinsky.
Temperature. M. “Nauka”, 1981, 159 pages
8. Ph.M. Kanarev. Forecast
of evolution of the fundamental physical investigations.
http://Kanarev.innoplaza.net . Book 2.
Webmaster: j_hartikka@hotmail.com
C New Fundamental Constant explained by Prof. Ph. M. Kanarev: http://Kanarev.constant.innoplaza.net
<< Kanarev´s Page In Russian >>