<<
Back to Kanarev's Physchemistry Book Index
8.2. Calculation of the Spectrum of the Hydrogen
Atom
Let us insert ![]() and n=2, 3, 4… into
the formulas (206) and (207). As a result, we’ll have the theoretical values
and n=2, 3, 4… into
the formulas (206) and (207). As a result, we’ll have the theoretical values ![]() (theor.) of energies
of the photons being absorbed or emitted by the electron during its energy
transitions in the hydrogen atom, which practically completely coincide with
the experimental values
(theor.) of energies
of the photons being absorbed or emitted by the electron during its energy
transitions in the hydrogen atom, which practically completely coincide with
the experimental values ![]() (exper.) of these
energies and binding energy
(exper.) of these
energies and binding energy ![]() of this electron with
the atomic nucleus (Table 5).
of this electron with
the atomic nucleus (Table 5).
Table 5.
Spectrum of the hydrogen atom
|
Volumes |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
10.20 |
12.09 |
12.75 |
13.05 |
13.22 |
|
|
eV |
10.198 |
12.087 |
12.748 |
13.054 |
13.220 |
|
|
eV |
3.40 |
1.51 |
0.85 |
0.54 |
0.38 |
It appears from the law of spectroscopy (207) that energies of the
photons being absorbed and emitted during the transition of the electron
between the energy levels ![]() and
and ![]() are calculated
according to the formula [33]
are calculated
according to the formula [33]
![]() (216)
(216)
Let us give the results of the calculation (Table 6) according to this
formula of the energies of the photons ![]() (theor.)
being emitted or absorbed by the electron of the hydrogen atom at the interlevel transitions
(theor.)
being emitted or absorbed by the electron of the hydrogen atom at the interlevel transitions ![]() and
and ![]() as compared with the
experimental
as compared with the
experimental ![]() (exper.) data.
(exper.) data.
Table 6. Energies of interlevel transitions of
the electron of the hydrogen atom
|
Levels |
n, n+1 |
2...3 |
3...4 |
4...5 |
5...6 |
6...7 |
7...8 |
|
|
eV |
1.89 |
0.66 |
0.30 |
0.17 |
0.10 |
0.07 |
|
|
eV |
1.888 |
0.661 |
0.306 |
0.166 |
0.100 |
0.065 |
Let us note that binding energies ![]() of the electron with
the atomic nucleus are given in Table 5. The rest energies of the photons being
emitted or absorbed during the energy transitions of the electron are given in
Tables 5 and 6.
of the electron with
the atomic nucleus are given in Table 5. The rest energies of the photons being
emitted or absorbed during the energy transitions of the electron are given in
Tables 5 and 6.
The
formula (216) gives the possibility to calculate the energies of the photons
being absorbed and emitted during any energy transition of the electron. For
example, when the electron goes from the third to the tenth energy level, it
absorbs the photon with the energy, which is calculated according to the
formula
![]() (217)
(217)
If the
electron goes from the fifteenth to the fifth energy level, it emits the photon
with the energy of
![]() (218)
(218)
Thus, these formulas give the possibility to calculate energy of the
absorbed and emitted photon by the electron during its transition between any
energy levels.
8.3. Calculation of the Spectra of the Hydrogen-like
Atoms
The
atoms, which have one electron, are called the hydrogen-like atoms. We have
shown that binding energy of the hydrogen atom at the time of its stay on the
first energy level is equal to ionization energy of this atom. The same
regularity is observed with all hydrogen-like atoms, i.e. the atoms, which have
one electron [18], [26], [53].
As in the atoms, which have many electrons, the electrons having the largest ionization energy are the
nearest electrons to the atomic nucleus, we have called them the first
electrons in our previous publications. Our further investigations have shown
that this numeration makes the further mathematical models for the calculation
of the spectra of the atoms with many electrons more complicated, we return to
the numeration of the electrons, which originates from the numeration of the
potentials of ionization of the atoms and ions [18], [26], [33], [53], [66],
[68], [69], [70], [75], [98], [99], [109].
For
example, the helium atom has two electrons. One has ionization energy 54.416 eV
and another 24.587 eV. Taking into consideration the above-mentioned facts
we’ll consider the electron with less ionization energy of 24.587 eV to be the
first electron of the helium atom and the electron with larger energy of 54.416
eV to be the second one. It means that lithium, the next element, will have the
electron with ionization energy of 5.392 eV to be the first one, the electron
with ionization energy of 75.638 eV to be the second one and the electron of
122.451 eV to be the third one. We’ll accept similar numeration of the
electrons for other chemical elements.
It
is known that the number of chemical element Z in Mendeleyev’s law corresponds
to the number of the protons in the atomic nucleus, and binding energy of the
electron of the hydrogen-like atom at the time of its stay on the first energy
level is proportional to square of the number of the protons in the nucleus.
Binding energy of the electron with
the proton (nucleus) of the hydrogen atom, which corresponds to the first
energy level, is equal to 13.598 eV. It means that binding energy ![]() of the electron of
the hydrogen-like atom of any other element corresponding to the first energy
level, will be equal to
of the electron of
the hydrogen-like atom of any other element corresponding to the first energy
level, will be equal to
![]() (219)
(219)
The theoretical and experimental values of binding energies of the
electrons of the hydrogen-like atoms, which correspond to their first energy
levels, are given for some chemical elements below (Table 7).
Table 7.
Theoretical and experimental values of binding energies of the electrons of the
hydrogen-like atoms, which correspond to their first energy levels
|
Chemical elements |
Number of element Z |
Binding
energies |
|
|
|
|
experiment |
theory |
|
H |
1 |
13.598 |
- |
|
He |
2 |
54.416 |
54.392 |
|
Li |
3 |
122.451 |
122.382 |
|
Be |
4 |
217.713 |
217.568 |
|
B |
5 |
340.217 |
339.950 |
|
C |
6 |
489.981 |
489.528 |
|
N |
7 |
667.029 |
666.302 |
|
O |
8 |
- |
870.272 |
At
present, it is considered that with the increase of the number of the protons
in the nucleus the number of the neutrons is increased as well as the mass of
the nucleus. It causes the increase of gravitational forces influencing the
electron. As a result, it is supposed that the gravitational forces begin to
influence the processes of absorption and emission of the photons, but the
relations (219) does not take it into account. That’s why the divergence between
the experimental values of binding energies of the electrons of the
hydrogen-type atoms and the results of the theoretical calculations (Table 7).
But later on we’ll see that the reason of this divergence is different.
Let us introduce a very important notion. Let us suppose that a
stationary energy level of the electron in the atom is such energy level, on
which the electron can absorb such photon when its binding energy with the
nucleus becomes equal to zero, and it will become free. Then binding energies
of the electrons of the hydrogen-like atoms corresponding to stationary energy
levels will be calculated according to the formula
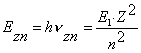 . (220)
. (220)
Symbol ![]() denotes the own
frequency of the photon emitted by the electron when it moves from the
stationary energy level n to free state.
denotes the own
frequency of the photon emitted by the electron when it moves from the
stationary energy level n to free state. ![]() =13.598 eV is ionization energy of hydrogen atom. The results
of the calculation according to the formula (220) are given in Table 8.
=13.598 eV is ionization energy of hydrogen atom. The results
of the calculation according to the formula (220) are given in Table 8.
Table 8.
Theoretical and experimental values of binding energies of the electrons with
nuclei of the hydrogen-like atoms corresponding to the stationary energy levels
|
Z |
Ele-ment |
Determination method |
Energies of stationary levels, eV |
|||
|
|
|
|
n=1 |
n=2 |
n=3 |
n=4 |
|
1 |
H |
Exper. Theor. |
13.598 - |
3.398 3.399 |
1.508 1.511 |
0.848 0.849 |
|
2 |
He |
Exper. Theor. |
54.416 - |
13.606 13.604 |
6.046 6.046 |
3.396 3.401 |
|
3 |
Li |
Exper. Theor. |
122.451 - |
30.611 30.613 |
13.601 13.607 |
7.651 7.653 |
|
4 |
Be |
Exper. Theor. |
217.713 - |
54.423 54.428 |
24.183 24.190 |
13.613 13.607 |
|
5 |
B |
Exper. Theor. |
340.217 - |
85.047 85.054 |
37.797 37.801 |
21.257 21.263 |
|
6 |
C |
Exper. Theor. |
489.981 - |
122.461 122.495 |
54.431 54.446 |
30.611 30.624 |
|
7 |
N |
Exper. Theor. |
667.029 - |
166.689 166.757 |
74.089 74.114 |
41.669 41.689 |
We’ll not calculate the spectra of the electrons of the hydrogen-like
atoms of all chemical elements. Let us
give only the method of the calculation for some of them. For example, let us
calculate the spectrum of the electron of the hydrogen-like atom of lithium
(the third one) corresponding to its second stationary energy level. The third
electron of this atom has the largest ionization energy ![]() . It is equal to binding energy of this electron with the
atomic nucleus
. It is equal to binding energy of this electron with the
atomic nucleus ![]() corresponding to the
first energy level
corresponding to the
first energy level ![]() 122.451 eV. If we
insert
122.451 eV. If we
insert ![]() =2, 3, 4, ……. in the formulas (206) and (207), we’ll find
(Table 9).
=2, 3, 4, ……. in the formulas (206) and (207), we’ll find
(Table 9).
Table 9.
Spectrum of the third electron of the lithium atom and its binding energies ![]() with the atomic
nucleus on the stationary energy levels
with the atomic
nucleus on the stationary energy levels
|
Values |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
91.84 |
108.84 |
114.80 |
117.55 |
119.05 |
|
|
eV |
91.84 |
108.85 |
114.80 |
117.55 |
119.05 |
|
|
eV |
30.61 |
13.60 |
7.65 |
4.80 |
3.40 |
The relation (207) was called by us a law of formation of the spectra of
the atoms and the ions, because before the determination of this law the
spectra of hydrogen-like atoms were calculated with the help of
Balmer-Rydberg’s equation or Schroedinger’s equation, and in order to calculate
the spectra of all further electrons, the approximate numerical methods were
used [9]. The equation (207) gives the possibility to calculate the spectra of
all electrons, but under certain conditions. Let us consider these conditions
in detail taking the calculation of the spectrum of the first electron of
helium atom as an example.
8.4. Calculation of the Spectrum of the Helium Atom
The
helium atom has two electrons. Ionization energy of the first one is ![]() =24.587 eV, and ionization energy of the second one is
=24.587 eV, and ionization energy of the second one is ![]() =54.416 eV [5].
=54.416 eV [5].
The state of the helium atom when
both its electrons are on the first energy levels is called the main unexcited
one. The second electron remains on the first energy level till the first
electron remains in the atom. Once the first electron leaves the atom, the
second electron passes to an excited state. Excitation energy is the energy of
the absorbed photon. It is equal to the difference between ionization energy ![]() of the electron and
binding energy of the electron with the atomic nucleus corresponding to the
energy level, to what the electron passes after the photon is absorbed. We call
such levels the stationary ones.
of the electron and
binding energy of the electron with the atomic nucleus corresponding to the
energy level, to what the electron passes after the photon is absorbed. We call
such levels the stationary ones.
Taking into consideration the
above-mentioned mentioned facts, let us present a row of the stationary energy
levels of the second electron of the helium atom and binding energies of the
electron with the nucleus corresponding to them and excitation energies ![]() (Table 10) [18],
[26], [53].
(Table 10) [18],
[26], [53].
Table 10. Energy indices of
stationary energy levels of the second electron of the helium atom
|
Number of
the level, n |
Binding
energy
|
Excitation
energies
|
|
1 |
54.416 |
0.00 |
|
2 |
13.60 |
40.81 |
|
3 |
6.09 |
48.37 |
|
4 |
3.39 |
51.02 |
|
5 |
2.17 |
52.24 |
|
6 |
1.51 |
52.90 |
|
7 |
1.11 |
53.31 |
|
8 |
0.85 |
53.57 |
|
9 |
0.67 |
53.74 |
|
10 |
0.55 |
53.87 |
|
11 |
0.45 |
53.97 |
|
12 |
0.38 |
54.04 |
|
… |
… |
… |
|
- |
0.00 |
54.416 |
The helium atom with one electron is
in ionized state, that’s why it is called a helium ion. We have already shown
that regularity of the change of the energies of the stationary energy levels
is the same with all atoms, which consist of a nucleus and one electron. The
spectra of such ions are calculated according to the mathematical model (207)
of the law of formation of the spectra of the atoms and the ions [33].
We’d like to draw the attention of
the readers to the main fact: the possibilities of Schroedinger’s equation
concerning the spectrum calculation are finished with hydrogen-like atoms.
Schroedinger’s equation does not give an opportunity to calculate the spectrum
of the first electron of helium atom. Let us consider the possibility of our
mathematical model (207) of formation of the spectra of the atoms and the ions
to calculate the spectrum of the first electron of the helium atom.
For this purpose, let us write from
the reference book [5] the excitation energies of the first electron of the
helium atom, which correspond to the stationary energy levels. At ![]() =24.587 eV we have (Table 11).
=24.587 eV we have (Table 11).
Table 11. Energy indices of
stationary energy levels of the first electron of the helium atom
|
Number of
the level, n |
Binding
energy
|
Excitation
energies
|
|
1 |
? |
? |
|
2 |
3.627 |
20.96 |
|
3 |
3.367 |
21.22 |
|
4 |
1.597 |
23.01 |
|
5 |
1.497 |
23.09 |
|
6 |
0.847 |
23.74 |
|
7 |
0.547 |
24.04 |
|
8 |
0.377 |
24.21 |
|
9 |
0.277 |
24.31 |
|
10 |
0.217 |
24.37 |
|
11 |
0.167 |
24.42 |
|
12 |
0.137 |
24.45 |
|
13 |
0.117 |
24.47 |
|
14 |
0.097 |
24.49 |
|
15 |
0.077 |
24.51 |
|
16 |
0.067 |
24.52 |
|
… |
? |
59.67 |
We’d like to remind that binding
energies ![]() of the
first electron with the atomic nucleus are determined as the difference between
the ionization energy
of the
first electron with the atomic nucleus are determined as the difference between
the ionization energy ![]() =24.587 eV and the excitation energies
=24.587 eV and the excitation energies ![]() being equal to the
energies of the absorbed photons or emitted photons
being equal to the
energies of the absorbed photons or emitted photons ![]() (Table 11).
(Table 11).
The last line in Table 8 looks
abnormal. Why the maximal excitation energy of 59.67 eV is larger than
ionization energy not only of the first electron (![]() =24.587 eV), but of the second one (
=24.587 eV), but of the second one (![]() =54.416 eV)? It is not simple to get the answer to this
question, but we’ll try to formulate the first hypothetical explanation of the
noted anomaly later on.
=54.416 eV)? It is not simple to get the answer to this
question, but we’ll try to formulate the first hypothetical explanation of the
noted anomaly later on.
The accuracy of the experimental
data of spectroscopy plays a decisive role in our search, because we’ll form
further notions concerning a picture of the interaction of the first electron
with the nucleus of the helium atom on their basis.
We’d like to note that in the
reference books [5] and [25] the experimental values of ionization energies are
determined with the accuracy up to the third character, and the excitation
energies of the stationary energy levels are determined with the accuracy up to
the second character. The writers of the reference books note that the value of
the second character of excitation energies differs with various authors by ±0.02 eV and sometimes even more.
Consequently, in order to determine
an empirical law, which forms a series of excitation energies of the stationary
energy levels of the first electron of the helium atom, it is necessary to
round the results of the calculations of binding energies to the second
character after point.
It is not all that should be taken
into consideration when analyzing the experimental data. Let us pay attention
to the following sentences in the reference book [5]: “Together with the
experimentally measured wavelengths, there are such lines in the tables being
suggested, which wavelengths are calculated according to the energy levels
taking into consideration the selection regulations. These are either the fine
structure lines, which are not yet discovered, or weak, rough measured spectral
lines. Validity of such calculation makes no doubts, because energy levels are
established according to the safely measured lines with the implementation of
the secondary standards”.
It is difficult to agree with such
method of the experimenters. Let us consider excitation energy of 23.01 eV
(Table 11), which corresponds to the fourth stationary energy level. It is not
available in the reference book [5]; in the reference book [25] it is given
without a line brightness designation, i.e. as a very weak or unobserved. What
should we do in this case? It is wise not to take it into consideration for the
time being during the search of regularity of formation of excitation energies,
which correspond to the stationary energy levels. Excitation energy being equal
to 20.96 eV is in the same position. That’s why let us exclude it from our
consideration.
At once, let us pay attention to the
fact how they have got the empirical law for the calculation of binding
energies of the first electron of helium atom given in Table 12, ![]() coinciding completely
with the law (206), which forms binding energies of the electrons of
hydrogen-like atoms. For this purpose, energy of 3.37 eV corresponding to
excitation energy of 21.22 eV in Table 11 was taken and multiplied by 4. The
number
coinciding completely
with the law (206), which forms binding energies of the electrons of
hydrogen-like atoms. For this purpose, energy of 3.37 eV corresponding to
excitation energy of 21.22 eV in Table 11 was taken and multiplied by 4. The
number ![]() =13.468 eV being obtained was the binding energy
corresponding to the first energy level of the first electron of the helium
atom. Of course, it is fictitious
energy, but a variety of energies formed in this case (Table 12, the last
column) coincides completely with a variety of the corresponding experimental
values confirming competence of exclusion of excitation energies of 20.96 eV
and 23.01 eV from this variety. The result being obtained shows that binding
energy of the fist electron of helium atom corresponding to the first energy
level of
=13.468 eV being obtained was the binding energy
corresponding to the first energy level of the first electron of the helium
atom. Of course, it is fictitious
energy, but a variety of energies formed in this case (Table 12, the last
column) coincides completely with a variety of the corresponding experimental
values confirming competence of exclusion of excitation energies of 20.96 eV
and 23.01 eV from this variety. The result being obtained shows that binding
energy of the fist electron of helium atom corresponding to the first energy
level of ![]() =13.468 eV is not equal to ionization energy of this
electron
=13.468 eV is not equal to ionization energy of this
electron ![]() =24.587 eV.
=24.587 eV.
Table 12. Binding energies ![]() of the first electron
of the helium atom with its nucleus being determined experimentally and theoretically
of the first electron
of the helium atom with its nucleus being determined experimentally and theoretically
|
Energy
level number, n |
Excitation
energy
|
Energy of
binding, eV |
|
|
experiment |
theory
|
||
|
1 |
24.586 |
? |
13.47 |
|
2 |
21.22 |
3.37 |
3.37 |
|
3 |
23.09 |
1.50 |
1.50 |
|
4 |
23.74 |
0.85 |
0.85 |
|
5 |
24.04 |
0.55 |
0.55 |
|
6 |
24.21 |
0.38 |
0.38 |
|
7 |
24.31 |
0.28 |
0.28 |
|
8 |
24.37 |
0.22 |
0.22 |
|
9 |
24.42 |
0.17 |
0.17 |
|
10 |
24.45 |
0.14 |
0.14 |
|
11 |
24.47 |
0.10 |
0.10 |
|
12 |
24.49 |
0.09 |
0.09 |
|
13 |
24.51 |
0.08 |
0.08 |
|
14 |
24.52 |
0.07 |
0.07 |
The results of this Table demand a
return to the experiment connected with the determination of the spectrum of
the first electron of helium atom in order to determine availability of lack of
experimental lines, which correspond to energies 20.96 eV and 23.01 eV.
A question arises: why do the values
of ionization energy ![]() and binding energy
and binding energy ![]() with the nucleus
corresponding to the first energy level of the second electron of the helium
atom coincide (
with the nucleus
corresponding to the first energy level of the second electron of the helium
atom coincide (![]() =54.416 eV), and the values of the first electron fail to coincide
(
=54.416 eV), and the values of the first electron fail to coincide
(![]() =24.587 eV and
=24.587 eV and ![]() =13.468 eV)? We have failed to find the reply to this
fundamental question, and we address it to the future investigators.
=13.468 eV)? We have failed to find the reply to this
fundamental question, and we address it to the future investigators.
An interesting and chargeable moment
comes. If the mathematical model (207) is in fact a law of formation of the
spectra of the atoms and the ions, we should get the experimental values of
excitation energies corresponding to the stationary energy levels with its
help. If we insert ![]() =24.587 and
=24.587 and ![]() =13.468 into the formulas (206) (207), we’ll get (Table 13).
=13.468 into the formulas (206) (207), we’ll get (Table 13).
Table 13. Spectrum of the first
electron of the helium atom
|
Valumes |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
21.22 |
23.09 |
23.74 |
24.04 |
24.21 |
|
|
eV |
21.22 |
23.09 |
23.74 |
24.05 |
24.21 |
|
|
eV |
3.37 |
1.50 |
0.84 |
0.54 |
0.37 |
Then we’ll get the spectra of other
atoms with many electrons using the determination method ![]() of binding of the
electron with the nucleus corresponding to the fist energy level worked out
with the implementation of the analysis of the spectrum of the first electron
of the helium atom.
of binding of the
electron with the nucleus corresponding to the fist energy level worked out
with the implementation of the analysis of the spectrum of the first electron
of the helium atom.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index