<<
Back to Kanarev's Physchemistry Book Index
5.4. Derivation of Mathematical Models, which Describe Behaviour of
the Photon
Some investigators [122], [149], [159] have noted that the photon has latent
parameters. If it were possible to find them, all (28-34) mathematical
relations describing its behaviour would be derived analytically. Let us try to
find these parameters.
As the photon model is rather complicated (Fig. 5), it is difficult to
find the relations (28-34). But if we take into consideration that the photon
has the plane of polarization, the movement of its centre of masses in this
plane as well as the movement of the centres of masses of its six
electromagnetic fields can be accompanied by rolling of the conventional
circumferences, which kinematics and energy parameters will be equal to the
corresponding parameters of the photon. The centre of mass M of the photon
makes a complete oscillation 
in the interval of
the length of its wave (Fig. 6); that’s why radius 
(the first latent
parameter) of the conventional circumference, which describes the motion of
this centre in the interval of the length of one wave, will be determined
according to the formula (Fig. 6) [8], [18], [26]:
.
(36)
The second conventional circumference will be the kinematics equivalent
of the group motion of the centres of mass of six electromagnetic fields of the
photon. Its radius 
(the second latent
parameter) is determined from the condition of a turn of the centre of mass of
each electromagnetic field of the photon through the angle 
in the interval of
each length of its wave (Fig. 6).
(37)
If angular velocity of the conventional circumference, which describes
the movement of the centre of mass M of the photon in relation to its
geometrical 
, is 
(the third latent
parameter) and angular velocity of the conventional circumference, which described
the motion of the centre of masses of each electromagnetic field, is 
(the fourth latent
parameter) and the linear frequency is 
, the period of oscillations of the centre of masses of the
photon will be determined according to the formulas (Fig. 6):
(38)
We have from it:
(39)
(40)
Binding relation between the wavelength 
, which describes the centre of mass of the photon and radius
of its rotation,
shows that the photon has six electromagnetic fields connected with each other
according to the circular circuit (Fig. 6).
(41)
Kinematical equivalence between the
motion of the complicated electromagnetic structure of the photon and the
conventional circumferences with radii 
and 
gives the opportunity
to derive the postulated mathematical
relations (28-34), which describe its behaviour. The latent unobserved
parameters of the photon take part in the intermediate mathematical conversions
and vanish in the final formulas.
As the small conventional circumference of radius 
moves in the plane of
rotation of the photon without sliding, velocity of any of its points will be
equal to velocity of its centre 
and group velocity of
the photon. Using relations (36) and (39), we’ll have:
(42)
which corresponds to the relation (29).
The
same result is given by the relations (37) and (40) of the second conventional circumference
of radius 
.
(43)
Now we see that the derivation of the relation (29) not only agrees with
the photon model (Fig. 5) and mechanics of its movement, but also explains
corpuscular and wave properties of the photon.
When deriving the relations (28), let us pay attention to the fact that
kinetic energy of motion of the photon with mass is equivalent to kinetic
energy of rolling of the conventional circumferences with the same masses m,
which are distributed equally in their length. Total kinetic energy of the
conventional circumference will be equal to the sum of kinetic energies of
their translational motion and rotation in respect to the geometric centre 
. (44)
We’ll have the same result if we
use the second conventional circumference of radius 
.
(45)
We’ll reduce the equation (44) to
(28)
, (46)
here
.
(47)
As it is clear, the latent parameters give the opportunity to derive the
main mathematical relations of quantum mechanics, which describe behaviour of
the photon, from the laws of classical mechanics. The conventional
circumferences allow to determine the group pulse of the photon.
, (48)
or
.
(49)
From this one it is easy to obtain the
corpuscular version of the Louis de Broglie’s
relation
. (50)
We’ll rewrite this as
.
(51)
In the left part of the equation (51) we have the product of the impulse
of the photon and its
wave-length 
, and on the right part we have Planck’s constant 
. Heisenberg’s uncertainty relation originates from it:
.
(52)
Let us rewrite this inequality in
an extended from.
. (53)
As the photon displays its pulse in the interval of each wave-length,
and its size is more than two wave-lengths (Fig. 5), the values 
and 
in inequality (53)
will be more than 2 each. If we assume that 
and 
and substitute these
values into inequality (53), we’ll have
. (54)
Usually the inequality of the
uncertainty principles is written as
,
(55)
or
. (56)
If we assume that 
and 
, we’ll obtain
, or 
(57)
Thus, the model of the photon restricts accuracy of experimental
information being obtained with its help [18], [26], [116]. It is explained by
the fact that the dimensions of the photon are some what larger than two
lengths of their waves. It means that
the photon cannot transmit a size of geometrical information, which is
less than two lengths of its wave or two radii of rotation as it appears from
Heisenberg’s inequality.
If we examine the object with the help of the photon with the specified
wavelength, we cannot get geometrical information concerning the object, which
would be equal to the wavelength of the photon being used or be less than it.
If the photon with smaller wavelength is used in order to get the same
information, accuracy of geometrical information will be increased. It
restricts physical sense of
Heisenberg’s inequality greatly. If this inequality is referred to experimental
information being obtained with the help of the photon, it is just only within
the framework of one length of its wave or one radius of rotation.
Let us recollect the statement of J. Marion: “If some day it is proved
that the principle of ambiguity is incorrect, we should anticipate complete
alteration of physical theory” [148]. The information obtained by us shows that
Heisenberg’s inequality restricts accuracy of experimental information only, it
does not restrict accuracy of theoretical information. J.B. Marion’s prophecy
makes sense.
5.5. Kinematics of the Photon
Let us begin with the derivation of the equations of centroidal motion 
of the photon. As
centre of mass of the photon moves in the polarization plane and within the
framework of the space-matter-time
unity axiom, it is necessary to have two parametric equations in order to
describe its motion along wave track.
As the centre of mass 
of the photon moves
in relation to an observer and in relation to geometric centre 
of the model, for the
complete description of such motion it is necessary to have two reference
systems: stationary reference system 
and moving reference
system 
.
Amplitude of oscillation A of the centre of mass M of the photon will be
equal to radius 
of its rotation in
reference to geometrical centre 
of the photon. From
Fig. 6 we have [4], [8], [18], [26]
. (58)
Let us pay attention to a small value of amplitude of oscillation of the
centre of mass of the photon in fractions of the length of its wave or radius
of rotation 
.
The equations of centroidal motion M of the photon in relation to moving
reference system 
have the
form:
;
(59)
.
(60)
If the photon
moves in relation to the stationary reference system with velocity 
, the equations of such motion will have the form [4]:
;
(61)
.
(62)
Thus, the main property of the equations (61) and (62), which describe
motion of the centre of mass of the photon is in the fact that they describe
motion of this centre within the framework of
the space-matter-time unity axiom. It should be noted that Louis de
Broglie’s equation (34) is deprived of this property. If we take into account
the relations (39) and (40), we’ll get [18], [26], [109], [116]:
(63)
(64)
where 
Irregularity of velocity of centre of mass of
the photon originates from this formula, in which electrical constant 
and magnetic constant 
are introduced easily.
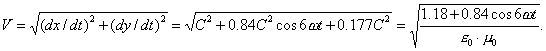(65)
The graph of velocity (65) of the centre of mass of the photon is shown
in Fig. 7.
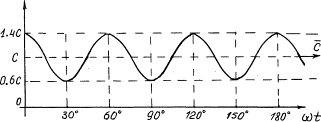
Fig. 7. Graph of velocity of the centre of mass
of the photon
As it is clear, velocity of the centre of mass M of the photon is
changed in the interval of the wavelength or the oscillation period from 
to 
in such a way that
its mean remains constant and equal to 
.
The equations of centroidal motion 
of one of electromagnetic
fields of the photon in relation to moving reference system 
(Fig. 6) will have
the form:
; (66)
. (67)
The
absolute motion of one electromagnetic
field of the photon, i.e. the motion in relation to the stationary reference
system 
, assumes the form:
; (68)
. (69)
These equations give the opportunity to determine all kinematic
characteristics of the centres of mass of electromagnetic fields of the photon.
But for us, it is more interesting to see the track (68), (69) described by these centres in
relation to the stationary reference system, i.e. in relation to the observer.
It is given in Fig. 8. The form of the track in the area of point 
is of special
interest (Fig. 6). This is the area of location of instantaneous centre of
velocities during rolling motion of a large conventional circumference [18],
[26].
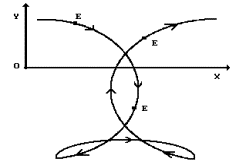
Fig. 8. Track of centroidal motion E1
of one of electromagnetic fields of the photon
A compound track of the centre of mass of each electromagnetic field of
the photon (Fig. 8) forms undulatory motion of its centre of mass and
straightness of motion of the whole photon. It will become a subject of future
investigations of electrodynamics of the photon.
Thus, we have got the equations (61) and (62), which describe the photon
motion more precise than Louis de Broglie’s equations (6), (34) and
Schroedinger’s equations (7). But if more precise mathematical relations take
place for the description of behaviour of some object, they should contain less
precise relations and be their consequences. The relations (61) and (62)
describing motion of the centre of mass of the photon should fulfil this
requirement.
In order to get the wave equation (34), it is necessary to move the
process of the description of motion of the centre of masses of the photon
outside the space - matter - time unity axiom. For this purpose, it is necessary
to take one of the equations (61) and (62), for example, the equation (62).
We’d like to draw the attention of the reader to the fact that this operation
automatically takes the process of the description of motion of the centre of
masses of the photon outside the space - matter - time unity axiom
.
(70)
In order to bring this equation to the form (34), it is necessary to introduce the coordinate x into this equation
using the phase difference for this purpose.
.
(71)
Taking into account that 
and 
, we have
.
Let us designate 
therefore
(72)
Now it is clear that the main reason for
the theoretical spreading of the de Broglie wave packet is explained by the
independence of coordinate x from time 
and the lack of
correspondence of de Broglie’s
equation with the space - matter - time
unity axiom. Equations (61) and (62) have no such disadvantage.
It is not difficult to show that equation (72) is reduced easily to
Schroedinger’s equation (9) [18], [26], [114], [144]. For this purpose, let us
get frequency 
and wavelength 
from the formulas
(28) and (30).
,
(73)
. (74)
Let us introduce a new designation of the function (72) and substitute
values (73) and (74) into it.
(75)
When 
is fixed, bias 
is a harmonic
function of time; when 
is fixed, it is a
function of coordinate 
.
If we differentiate the equation (75) twice according to 
, we’ll find
(76)
If behaviour of the electron in the atom is described with the help of the
relation (76), it should be taken into consideration that its kinetic energy 
and pulse 
are connected with
the relation
. (77)
Hence
.
(78)
If we substitute the result (78) into the equation (76), we’ll have
(79)
It is known that full energy of the electron 
(123) is equal to the
sum of kinetic energy 
and potential energy 
, i.e.
.
(80)
If we take it into consideration, the equation (79) get the form of
Schroedinger’s differential equation (9)
(81)
It appears from the above-mentioned facts that the result of the
solution of the equation (81) is function (72) operating outside the framework
of the space-matter-time unity axiom.
Thus, we have derived all the basic mathematical models of quantum
mechanics postulated earlier and describing behaviour of the photon. We have
shown that Louis de Broglie’s equation (34) and Schroedinger’s equation (9)
operate outside the framework of the space-matter-time unity axiom.
Thus, we let all mathematical formulas alone, which are used for the
photon behaviour description for a long time. In this sense, we have nothing
new, we have only confirmed trustworthiness of these formulas and supplemented
them with the equations (61) and (62), which describe centroidal motion of the
photon within the framework of the space-matter-time unity axiom.
5.6. On the Way to Electrodynamics of the
Photon
It results from this that mass of the photon is formed by its
electromagnetic field [4], [8], [18], [26], [116]. That’s why the interaction
between these fields provokes the internal Newton and electromagnetic forces.
The forces localize the photon in space and provide its motion with constant
velocity. That’s why the main task of future electrodynamics of the photon is
to find these forces. As the equations
of motion of the centre of mass of the photon and the centres of masses of its
electromagnetic fields are known [4], [8], [18], [26], it is not difficult to
determine the Newton’s forces. For example, in order to determine the Newton’s
forces influencing the centre of masses of the photon, it is necessary to know
tangential and normal acceleration of its
centre of mass [101]. Tangential acceleration 
of motion of the
centres of masses of the photon will be equal to
(82)
Maximal value of tangential
acceleration is equal to 
.
Tangential force
influencing the
centre of masses of the photon will be equal to
(83)
Normal acceleration 
of the centre of
masses of the photon
. (84)
Normal or centrifugal force influencing the centre of masses of the
photon
. (85)
Full acceleration of the centre of masses of the photon
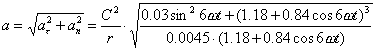. (86)
Let us note that maximal value of overall acceleration is equal to 
.
If we take into consideration that 
, resulting force influencing the centre of mass of the
photon will be defined in the following way
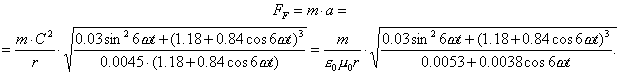(87)
Obviously, it is enough to think that the way to electrodynamics of the photon
is opened, but it will be not easy. Certainly, the photon model provokes a
large number of the new questions and requires the new answers for numerous
results of the experiments, in which behaviour of the photon is registered.
Nearly ten answers for such questions are available in the books [8], [18],
[26]. We give a part of them here. But prior to it, we’d like to attract
the attention of the readers to the
essence of dimensionality of Planck’s constant.
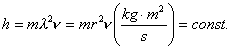(88)
In SI system this dimensionality corresponds to the following equal
notions of modern physics and mechanics: angular momentum, moment of momentum
and spin. It results from this that the law of conservation of angular momentum
governs persistence of Planck’s constant. It runs as follows: if the sum of
external forces influencing a rotating body is equal to zero, angular momentum
h (momentum of momentum, spin) of this body remains constant al the time.
5.7. Analysis of Experimental Results
1. Why do the photons fail to exist in rest?
Because the centre of photon masses M (Fig. 5) never coincides with its
geometrical centre 
. This lack of coincidence will create asymmetry between the
electromagnetic forced of the photon and forms the state of unstable
equilibrium, which causes its movement.
2. Why do the photons possess the properties of a wave and of a particle at the same time?
As the electromagnetic fields are closed along the round contour, the
photon obtains the properties of a particle, and the oscillations of the centre
of mass M of this particle relative to the geometrical centre 
impart the wave
properties to it (Fig. 5). As the photon surface is not a spherical one, but it
has a complicated curvilinear form, interacting with the objects, which form
diffraction and interference pictures they will be distributed on the screen
not at random, but in accordance with the surface form and the interaction
laws, which result from this.
3. Why do the photons move rectilinearly?
The linear movement of the photons takes place simultaneously with
rotary motion and translational motion; as a result, angular momentum is
formed, which keeps the photon on the straight-line trajectory. It should be
noted that angular momentum of the photon is its spin directed along the axis
of its rotation. This fact follows from dimensionality of Planck’s constant and
from the data analysis results of experimental spectroscopy. It contradicts
Maxwell’s theory, according to which the photon spin is directed along the
photon movement trajectory. It is a natural contradiction, because Maxwell’s
theory operates outside the framework of the space-matter-time unity axiom.
4. Why are the photons polarized?
They rotate in one plane, and the centrifugal forces of inertia
influencing the centres of the masses of electromagnetic fields of the photon
increase their radial dimensions and reduce the dimensions, which are
perpendicular to the plane of rotation. Due to it the photons acquire a form,
which is different from the spherical one and resemble the flat one.
5. Why do the photons possess no charge?
They consist of even quantity of direction different electrical and
magnetic fields, which make the total charge of the photon equal to zero.
6.
Why is angle of incidence of the photon equal to angle of reflection despite of
the rotation plane orientation (photon polarization)?
When
the photon contacts the reflecting plane, the photon is partially deformed and
acquires the form, which is almost a spherical one. But this is not all. The
calculations demonstrate that at the moment of reflection the photon has no
transversal component of a pulse. Thus, as the form of the photon is almost a
spherical one at the moment of reflection and there is only a longitudinal
pulse, the conditions are formed when the angle of incidence of the photon is
equal to the angle of reflection despite of the orientation of its plane of
rotation in the moment of reflection.
7.
Does the photon have velocity of light after reflection or creation or does it
move with acceleration at the beginning?
When reflected or born, the photon moves with accelerations as the
processes of creation and reflection are the transient processes, during which
it obtains the limit velocity after a definite quantity of oscillations.
8.
Does the photon lose energy during transient process?
Yes, it does mainly transferring it to an object, with which
it interacts. Compton effect proves it. Due to it the wavelength of the
reflected photon is increased. As it is clear from the relations 
, it is possible only when its mass m and oscillation
frequency v is reduced. The photon energy reduction is equal to the reduction
of its mass, and the reduction of mass leads to the reduction of density of
electromagnetic fields and the reduction of electromagnetic forces, which compress
the photon; due to it, the photon rotation radius is increased. Equality
between the electromagnetic forces and centrifugal forces of inertia
influencing the centres of masses of electromagnetic fields is restored due to
the reduction of angular momentum 
of rotation of the
centre of mass of the photon, and, consequently, the linear frequency 
of its oscillations.
It is the essence of the process of “reddening” of the photons in Compton
effect and in Doppler effect. The same phenomenon takes place when the photon
is born. Infrared and ultraviolet displacement of spectral lines in the
astrophysical observations is its proof.
9. What
is the nature of radio wave band of the scale of electromagnetic radiation?
A
radio wave band of radiation is a flux of photons, and a modelled radio wave is
a flux of photon pulses (Fig. 4).
10.
Why is the propagation distance of a surface radio wave is increased with the
increase of its length?
Due to the increase of the length of the radio wave, the number of the
photons, which form this wavelength (Fig. 4), is increased, and the possibility
of delivery of information by such wave is increased, despite of the fact that
a part of the photons is disseminated by the environment, and a part of them is
absorbed. If the wavelength is reduced, the number of the photons, which carry
it, is reduced, and the possibility of delivery of information to the receiver
is reduced.
11. In which way does a
radio wave with the length measured in kilometres transmit the information to
an aerial of the receiver, which sizes can have only several centimetres or
less?
It is possible to transmit the information by a radio wave, which
length is measured in kilometres, to
the aerial of the receiver by many factors of magnitude less than the length of
radio wave due to the fact that a set of single photons carries the wave.
That’s why in order to stimulate the atomic electrons of the aerial of the
receiver in the given sequence only several photons (Fig. 4) from this set
(waves) are enough to reach it.
12.
Why does relic emission possess the largest intensity in millimetre range?
It is due to the fact that in this range there exists a wavelength of
the largest infrared photon as far as the dimensions are concerned, but the
least one as far as mass is concerned
and all photons lose their mass gradually during their life and numerous
collisions and are converted into infrared photon with minimal mass (energy).
The wavelength of these photons is in millimetre range. It seems that relic
emission is an emission of obsolete photons.
13. What
electromagnetic emissions are in close vicinity with relic emission?
The emissions, which wavelength is greater than the wavelength of relic
emission, belong to a microwave range; the emissions with smaller wavelength
belong to an infrared range.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index